Wilcoxon Vorzeichen-Rang-Test
Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, Stand: 08.06.2019
Sie wollen zwei Mittelwerte aus abhängigen Stichproben vergleichen, aber die Voraussetzungen für den t-Test für verbundene Stichproben sind nicht erfüllt? Dann ist der Wilcoxon-Vorzeichen-Rang-Test eine Alternative.
Mit diesem Test können Sie die zentrale Tendenz (bei diesem Test in der Regel der Median) von zwei verbundenen Gruppen auch dann vergleichen, wenn die Voraussetzung der Normalverteilung nicht erfüllt ist.
Inhalt
- Beispiele für den Anwendungsbereich
- Auf welchen Grundprinzipien basiert der Test?
- Beispiel
- Ergebnisse des Tests
- Wie ermitteln Sie die Effektstärke?
- Welche Nullhypothese hat der Test?
- Was sind die Voraussetzungen des Tests?
- Vorzeichen-Rang-Test bei ordinalskalierten Daten?
- Wie prüfen Sie die Voraussetzungen?
- Und wenn die Voraussetzungen nicht erfüllt sind?
- Aufruf in SPSS
- Interpretation der SPSS Auswertung
- Testergebnisse berichten
- Quellen
1. Beispiele für den Anwendungsbereich
Beispiel 1 (BWL): Sie wollen untersuchen, ob beim größten Unternehmen einer Branche die durchschnittliche Amtsdauer des Vorstandsvorsitzenden länger ist als beim jeweils zweitgrößten Unternehmen derselben Branche, allerdings sei die Amtsdauer nicht normalverteilt. Dann können Sie den Vorzeichen-Rang-Test heranziehen.
Beispiel 2 (Psychologie): Sie wollen prüfen, ob sich die Lebenszufriedenheit von Versuchspersonen erhöht, wenn sie ein Trainings-Programm zu mehr Optimismus aus der positiven Psychologie durchlaufen. Die Antworten auf der von Ihnen verwendeten Skala zur Lebenszufriedenheit seien aber nicht normalverteilt. Daher kommt der Vorzeichen-Rang-Test in Frage.
2. Auf welchem Grundprinzip basiert der Wilcoxon-Vorzeichen-Rang-Test?
Der Test gehört zu den nicht-parametrischen Verfahren. Es werden also keine Parameter (Mittelwert, Varianz) geschätzt, um den Test durchzuführen. Stattdessen werden die Ränge der Messwerte betrachtet.
Dazu werden zunächst aus den verbundenen Paaren der abhängigen Variable Differenzen berechnet. Bei einer Untersuchung mit Messwiederholung (siehe oben Beispiel 2) würde also die Differenz zwischen zweiter und erster Messung berechnet.
Dann werden alle Differenzwerte der abhängigen Variable der Größe nach geordnet, beginnend mit dem kleinsten Wert. Dabei wird das Vorzeichen noch nicht berücksichtigt, jedoch wird es notiert für einen späteren Schritt.
Nun werden diesen der Größe geordneten Differenzwerten Ränge zugewiesen, beginnend mit der kleinsten Differenz. Wenn die Differenz 0 beträgt, wird der Wert aus der Auswertung herausgenommen (wichtig: damit reduziert sich auch die Anzahl N).
Jetzt werden auch die Vorzeichen berücksichtigt: Es werden die Ränge getrennt aufsummiert für die Differenzen mit positiven Vorzeichen und die Differenzen mit negativem Vorzeichen. Es gibt als Ergebnis dieses Schrittes also eine Rangsumme der positiven Differenzen und eine Rangsumme der negativen Differenzen.
Wenn die Werte in den beiden verbundenen Gruppen im Wesentlichen gleich sind, dann gibt es ungefähr gleich viele positive und negative Differenzen und auch ähnlich viele hohe und niedrige absolute Differenzen. Das bedeutet dann auch zwei ungefähr gleich hohe Rangsummen für die beiden Vorzeichen.
Wenn aber die zentrale Tendenz (Median) der Differenz sich von 0 unterscheidet, dann wird die Summe bei einem der beiden Vorzeichen deutlich größer sein als beim anderen.
Bei der o.g. Bildung der Rangreihe kann noch ein Problem auftreten: Sogenannte verbundene Ränge. Es kann sein, dass ein Differenzwert mehr als einmal vorkommt, das nennt man Rangbindung. Dieses Problem wird beim Wilcoxon-Vorzeichen-Rang-Test meistens mit der Zuweisung von mittleren Rängen gelöst.
Beispiel: Der niedrigste von 0 verschiedene Differenzwert der abhängigen Variable tritt doppelt auf. Dann bekommt nicht eine Differenz den Rang 1 und die andere den Rang 2, sondern beide den Rang 1.5. Wenn es zu viele Rangbindungen gibt, reduziert das jedoch die Aussagekraft des Tests. Das gilt auch, wenn es zu viele Differenzen von 0 gibt.
Hinweis zu SPSS: Der Begriff Rangbindung ist bei diesem Test nicht völlig eindeutig. SPSS verwendet ihn etwas anders, nämlich für diejenigen Wertepaare, die gleich sind und deshalb gar keinen Rang zugewiesen bekommen.
3. Beispiel Wilcoxon-Vorzeichen-Rang-Test
Als Beispiel nehmen wir einen Fall mit Messwiederholung. Vor und nach einem Trainingsverfahren werden die Werte in einem Leistungstest erhoben und es soll getestet werden, ob sich die Leistungswerte (Anzahl richtig beantwortete Fragen) nach dem Test signifikant verändert haben. Sie gehen nicht davon aus, dass die Werte normalverteilt sind.
Bei den Personen wurden vor und nach dem Trainings-Programm folgende Werte erhoben:
| Person | vorher (t1) | nachher (t2) |
|---|---|---|
| 1 | 4 | 5 |
| 2 | 3 | 4 |
| 3 | 2 | 5 |
| 4 | 4 | 6 |
| 5 | 5 | 5 |
| 6 | 4 | 3 |
| 7 | 1 | 2 |
| 8 | 2 | 2 |
| 9 | 1 | 5 |
| 10 | 3 | 5 |
Arbeitsschritte, wenn Sie per Hand den Test berechnen:
1. Differenzwerte ermitteln zwischen den beiden jeweils verbundenen Untersuchungseinheiten.
2. Differenzen werden ohne Berücksichtigung des Vorzeichens aufsteigend geordnet. Das jeweilige Vorzeichen der Differenz wird jedoch notiert.
3. Entsprechend der Ordnung den Differenzen aufsteigende Ränge zugewiesen, beginnend bei 1 und endend bei N.
4. Jetzt kommen die Vorzeichen der Differenzen ins Spiel: Getrennt für die positiven Differenzen und die negativen Differenzen die Ränge aufsummieren.
| Person | Differenz | Rang | Rang positiv | Rang negativ |
|---|---|---|---|---|
| 5 | 0 | kein Rang | ||
| 8 | 0 | kein Rang | ||
| 1 | 1 | 2.5 | 2.5 | |
| 2 | 1 | 2.5 | 2.5 | |
| 6 | -1 | 2.5 | 2.5 | |
| 7 | 1 | 2.5 | 2.5 | |
| 4 | 2 | 5.5 | 5.5 | |
| 10 | 2 | 5.5 | 5.5 | |
| 3 | 3 | 7 | 7 | |
| 9 | 4 | 8 | 8 |
Sie sehen, dass es in diesem Beispiel sehr viele Rangbindungen gibt. Das kommt vor allem bei abhängigen Variablen vor, die auf einer relativ kurzen Skala gemessen werden.
Aus diesen Daten ergibt sich als Rangsumme für positive Ränge T+ = 33.5 und als Rangssumme für negative Ränge T- = 2.5 bei einem Umfang von N = 8 (2 Differenzen sind 0 und haben daher keinen Rang bekommen).
4. Ergebnisse des Tests
Die Teststatistik des Wilcoxon-Vorzeichen-Rang-Tests ist die kleinere der beiden Rangsummen T+ und T-. Im o.g. Fall ist dies also W = 2.5.
Wenn man den Test per Hand durchführt, wird dieser Wert mit dem kritischen Wert aus einer entsprechenden Tabelle verglichen.
Für größere Stichprobenumfänge kann man die Teststatistik über die Normalverteilung approximieren. Laut Gibbons und Chakraborti (2003) reicht es dafür, wenn mindestens 15 Wertepaare vorliegen.
Da moderne Computer auch einen exakten Test heute recht schnell berechnen können, sollte man hier aber eher einen höheren Wert für die Entscheidung genauer Test vs. Normalverteilungsapproximation heranziehen.
Im Beispiel oben ist der kritische Wert bei beidseitiger Testung für N = 8 und ein Signifikanzniveau von .05 der Wkrit = 3, so dass die Teststatistik mit W = 2.5 kleiner als der kritische Wert ist. Damit ist die Differenz der beiden Messzeitpunkte signifikant von 0 verschieden.
5. Wie ermitteln Sie die Effektstärke?
Der approximierte Wert basiert auf der Normalverteilung. Daher haben Sie mit ihm einen z-Wert zur Verfügung, der in SPSS auch standardmäßig mit ausgewiesen wird.
Und z-Werte können Sie leicht nach folgender Formel in das Effekstärkenmaß r umrechnen (mit N = n1 + n2, also der Anzahl der Beobachtungen, nicht der Anzahl der Paare laut Field, 2013 - allerdings gibt es zahlreiche Internetquellen, die besagen, dass es auf die Zahl der Datenpaare ankommt, insofern bin ich mir da nicht sicher, welche Aussage zutrifft.):
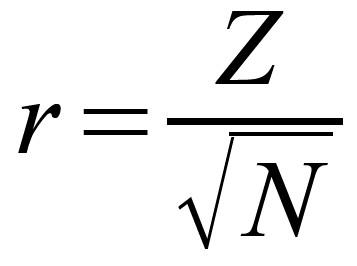
Diesen Wert können Sie dann in Relation zu den Effektstärkekonventionen nach Cohen (1992) setzen. Danach ist ein Wert von:
r = .50 ein starker Effekt,
r = .30 ein mittlerer Effekt,
r = .10 ein schwacher Effekt.
6. Welche Nullhypothese hat der Test?
Die Nullhypothese lautet, dass die Verteilung der Differenzen zwischen beiden Gruppen symmetrisch um Null ist. Die Nullhypothese lautet damit nicht: Beide verbundene Gruppen haben den gleichen Mittelwert oder Median!
Das sieht jetzt nach einem Widerspruch aus, denn oben wurde dieser Test als ein Test für zwei Mittelwerte bzw. Mediane vorgestellt. Wie kann das sein?
Man kann mit dem Wilcoxon-Vorzeichen-Rang-Test tatsächlich nur indirekt Unterschiede von Mittelwerten bzw. Medianen nachweisen. Denn was bedeutet es, dass die Differenz von zwei Gruppen symmetrisch um Null verteilt ist?
Dafür müssen vor allem zwei Dinge zutreffen:
1. Die Mittelwerte/Mediane sind in beiden verbundenen Gruppen gleich bzw. die Differenz ist gleich Null.
2. Die Verteilungen der Differenz ist symmetrisch.
Nur wenn beide Bedingungen erfüllt sind, gilt die Nullhypothese. Wenn einer der beiden Bedingungen nicht erfüllt ist, kann die Nullhypothese verworfen werden. Folge: Der Test wird ggf. signifikant.
Damit kann man Unterschiede der Mittelwerte in verbundenen Stichproben nur indirekt nachweisen:
Sie haben ein signifikantes Testergebnis. Damit wissen Sie, dass sich entweder die Mittelwerte/Mediane unterscheiden oder die Verteilung nicht symmetrisch ist oder beides. Um daraus auf unterschiedliche Mittelwerte zu schließen, brauchen Sie also eine zusätzliche Information: Dass die Verteilung der Differenz symmetrisch ist. Denn dann bleibt als Erklärung für die Signifikanz nur noch übrig, dass sich die Mittelwerte unterscheiden.
Und das führt uns direkt zu den Voraussetzungen dieses Tests.
7. Was sind die Voraussetzungen des Vorzeichen-Rang-Tests?
Auch nonparametrische Verfahren sind nicht völlig frei von Voraussetzungen. Bei diesem Test sind es insbesondere die folgenden beiden:
Voraussetzung 1:
Die Verteilung der Differenz der beiden Gruppen ist symmetrisch.
Voraussetzung 2:
Alle Untersuchungseinheiten innerhalb einer Gruppe (nicht: zwischen den Gruppen) sind unabhängig voneinander. (Das gilt eigentlich für alle Gruppenvergleiche, also auch ANOVA, t-Test, usw.)
Insbesondere die erste Voraussetzung müssen Sie gesondert vorab prüfen, wenn sie den Test durchführen, sonst kann er zu falschen Ergebnissen führen. Je stärker diese Voraussetzung verletzt ist, desto eher wird der Test signifikant, auch wenn gar keine Mittelwertsunterschiede vorliegen!
Außerdem müssen natürlich zwei verbundene Stichproben vorliegen, denn nur dafür ist dieser Test gedacht. Für den nonparametrischen Vergleich von zwei unabhängigen Stichproben gibt es andere Tests, vor allem den U-Test. Und die abhängige Variable muss mindestens ordinalskaliert (in der Regel aber intervallskaliert) und theoretisch kontinuierlich sein.
8. Vorzeichen-Rang-Test bei ordinalskalierten Daten?
Wenn man verschiedene Beiträge über den Wilcoxon-Vorzeichen-Rang-Test liest, dann bleibt häufig zu einer Frage eher Verwirrung zurück: Müssen die Daten intervallskaliert sein oder reicht auch Ordinalskalierung aus?
Die kurze Antwort:
In der Regel brauchen Sie eine Intervallskala, für ordinalskalierte Daten ist der Vorzeichentest geeignet, der eine etwas geringere Teststärke hat.
Die lange Antwort:
Diese Verwirrung beruht teilweise darauf, dass der Vorzeichen-Rang-Test nicht nur für zwei verbundene Stichproben eingesetzt werden kann. So wird der Wilcoxon-Vorzeichen-Rang-Test für eine Stichprobe z.B. eingesetzt, wenn Sie testen wollen, ob sich die abhängige Variable in einer Stichprobe signifikant von 0 bzw. einem festen Wert unterscheidet.
Die Voraussetzung für den Vorzeichen-Rang-Test ist, dass die Ränge mindestens ordinalskaliert sind. Das ist im Ein-Stichproben-Fall unproblematisch, denn dann können Sie bei einer ordinalskalierten abhängigen Variable dieser ohne Schwierigkeiten Ränge zuweisen, die wiederum ordinalskaliert sind.
Bei zwei verbundenen Stichproben kommt jedoch ein weiterer Schritt hinzu: Sie müssen vorher die Differenzen zwischen den jeweiligen Wertepaaren der beiden Stichproben ermitteln. Und Differenzen sind für ordinalskalierte Daten im Grundsatz nicht definiert, für Differenzbildungen braucht man Intervallskalierung.
Beispiel:
Sie haben eine Skala, die offensichtlich nur ordinalskaliert ist:
0: nie
1: häufig
2: sehr häufig
3. fast immer
4. immer
Diese Skala dürfte im Regelfall nicht sehr sinnvoll konstruiert sein, aber es gibt tatsächlich empirische Fragestellungen, für die man eine vergleichbar „schiefe“ Skala nimmt.
Diese Skala legen Sie zu irgendeiner Fragestellung z.B. jeweils beiden Ehepartnern vor und für zwei Paare bekommen Sie die folgenden Antworten:
Paar 1: er 0, sie 1
Paar 2: er 2, sie 4
Für das erste Paar wäre der rechnerische Differenzwert 1, für das zweite Paar 2. Aber es ist alles andere als sicher, dass der Unterschied zwischen „nie“ und „häufig“ (rechnerische Differenz = 1) kleiner ist als der Unterschied zwischen „sehr häufig“ und „immer“ (rechnerische Differenz = 2).
Insofern darf man bei ordinalskalierten Daten nicht die rechnerischen Differenzen nehmen und daraus die Ränge für den Vorzeichen-Rang-Test berechnen.
Es gibt allerdings zumindest theoretisch eine Möglichkeit, doch diesen Test in so einer Situation mit ordinalskalierte Daten in verbundenen Stichproben anzuwenden:
Sie vergleichen inhaltlich (nicht rechnerisch per Differenzbildung!) alle möglichen Paare von Testwerten und bringen alle möglichen Paarunterschiede insgesamt in eine Rangfolge. Das heißt, Sie entscheiden z.B. die o.g. Frage aus inhaltlichen Überlegungen: Was ist größer, der Unterschied zwischen „nie“ und „häufig“ oder der zwischen „sehr häufig“ und „immer“? Bei einer fünfstufigen Skala wie oben wären das beispielsweise 10 Paarvergleiche.
Wenn Sie das für alle Paare von Werten gemacht haben, dann können Sie diesen möglichen Abständen sinnvoll Ränge zuweisen und dann auch den Vorzeichen-Rang-Test anwenden.
Wenn das entweder inhaltlich nicht geht oder es zu aufwändig ist, dann bleibt Ihnen immer noch der Vorzeichen-Test.
9. Wie prüfen Sie die Voraussetzungen?
Zur Prüfung der wesentlichen Voraussetzung der Symmetrie der Differenzverteilung erstellen Sie ein Histogramm für die Differenzen. Das heißt, Sie erstellen eine neue Variable für die Differenz der abhängigen Variable in beiden verbundenen Gruppen und betrachten dann das Histogramm dieser neuen Variable. Wenn es eine im wesentlichen symmetrische Verteilung ist, dann können Sie den Test durchführen.
Die anderen Voraussetzungen prüfen Sie, bevor Sie überhaupt anfangen mit den Datenauswertungen. Denn sonst kommt der Wilcoxon-Vorzeichen-Rang-Test grundsätzlich nicht in Frage.
10. Und wenn die Voraussetzungen nicht erfüllt sind?
Eine Alternative ist der oben bereits erwähnte Vorzeichentest (sign test). Dieser ist ebenfalls nonparametrisch und die Verteilung der Differenzen muss anders als beim Wilcoxon-Vorzeichen-Rang-Test nicht symmetrisch sein. Allerdings hat der Vorzeichentest eine geringere Teststärke: Es ist also schwieriger, einen tatsächlich bestehenden Effekt nachzuweisen.
11. Aufruf Wilcoxon-Vorzeichen-Rang-Test in SPSS
Mit folgender SPSS-Syntax prüfen Sie die Voraussetzungen und rufen den Test auf:
*Vorauswertungen: Histogramm der Differenzen.
COMPUTE y_differenz= y2 - y1.
EXECUTE.
FREQUENCIES VARIABLES=y_differenz
/FORMAT=NOTABLE
/HISTOGRAM
/ORDER=ANALYSIS.
*eigentlicher Wilcoxon-Vorzeichen-Rang-Test:.
NPAR TESTS
/WILCOXON=y1 WITH y2 (PAIRED)
/STATISTICS DESCRIPTIVES QUARTILES
/MISSING ANALYSIS.
Wenn Sie eine gerichtete Hypothese haben und daher einseitig testen wollen, dann halbieren Sie den resultierenden p-Wert.
Den exakten Test können Sie ggf. so aufrufen (inkl. deskriptive Daten und Quartile/Median):
*Vorauswertungen: Histogramm der Differenzen.
COMPUTE y_differenz= y2 - y1.
EXECUTE.
FREQUENCIES VARIABLES=y_differenz
/FORMAT=NOTABLE
/HISTOGRAM
/ORDER=ANALYSIS.
*Exakter Wilxcoxon-Vorzeichen-Rang-Test:.
NPAR TESTS
/WILCOXON=y1 WITH y2 (PAIRED)
/STATISTICS DESCRIPTIVES QUARTILES
/MISSING ANALYSIS
/METHOD=EXACT TIMER(5).
Den Aufruf des Tests aus dem Menü finden Sie hier:
- ->Analysieren
- ->Nicht parametrische Tests
- ->Klassische Dialogfelder
- ->Zwei verbundene Stichproben
Mit der Schaltfläche "Exakt" (wenn diese in Ihrer SPSS-Version enthalten ist) können Sie den exakten Test aufrufen (Standard ist sonst die Approximation über die z-Verteilung).
Unter der Schaltfläche "Optionen" können Sie deskriptive Statistiken und Quantile (und damit auch den Median) aufrufen - wenn Sie das nicht schon in einem früheren Schritt getan haben, dann ist das jetzt sinnvoll.
12. Interpretation SPSS-Output zum Wilcoxon-Vorzeichen-Rang-Test
Ein Beispiel zur Interpretation der SPSS Auswertung finden Sie in folgender pdf-Datei:
Interpretation SPSS-Output Wilcoxon Vorzeichen-Rang-Test (pdf)
13. Testergebnisse berichten
Sie könnten die Ergebnisse eines Wilcoxon-Vorzeichen-Rang-Tests inkl. der Effektstärke beispielsweise so darstellen:
„Zum zweiten Messzeitpunkt war die Schulnote signifikant besser (Mdn = 3.15) als zum ersten Messzeitpunkt (Mdn = 3.53), z = - 3.16, p = .002. Mit r = .79 lag ein starker Effekt vor.“
(Diese Darstellung basiert auf der Approximierung mit der Normalverteilung. Wenn Sie bei kleinem N den exakten Test berichten, verwenden Sie statt des z-Wertes die Teststatistik W. Die wird zwar in SPSS nicht direkt berichtet, aber sie ist die kleinere der beiden Rangsummen.).
14. Quellen
Cohen, J. (1992). A power primer. Psychological bulletin, 112, 155-159. doi: 10.1037/0033-2909.112.1.155
Field, A. (2013). Discovering statistics using IBM SPSS statistics: And sex and drugs and rock 'n' roll (4th edition). Los Angeles, CA: SAGE.
Gibbons, J. D., & Chakraborti, S. (2003). Nonparametric statistical inference (4. ed.). New York, NY: Marcel Dekker.