Strukturgleichungsmodelle mit R lavaan
5. Longitudinale Messinvarianz für Längsschnitt-SEM
Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, 27.08.2023
Dieses Tutorial zeigt an einem konkreten Beispiel, wie Sie mit lavaan als Voraussetzung für eine Längsschnitt-SEM-Modell die longitudinale Messinvarianz prüfen können.
Video
(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)
1. Warum longitudinale Messinvarianz?
Wenn Sie ein Längsschnitt-SEM-Modell schätzen möchten, dann müssen Sie zunächst die longitudinale Messinvarianz prüfen. Das heißt Sie müssen prüfen, ob das Messmodell Ihrer latenten Variablen über die verschiedenen Messzeitpunkte gleich funktioniert (ob also auch wirklich zu jedem Zeitpunkt inhaltlich das gleiche gemessen wird). So kann beispielsweise bei Untersuchungen im Kinder- und Jugendalter zu verschiedenen Entwicklungszeitpunkten das gleiche Messinstrument in unterschiedlichem Maß das interessierende Konstrukt messen. Oder es kann Lern-/Übungseffekte geben, so dass zu einem späteren Messzeitpunkt die Fragen anders bearbeitet werden als zum ersten Messzeitpunkt.
2. Welche Arten von longitudinaler Messinvarianz gibt es?
Potentiell relevant sind die folgenden Arten der Messinvarianz:
- Konfigurale Messinvarianz: Gleiche Faktorstruktur
- Metrische Messinvarianz: Gleiche Ladungen (anderer Namen: Weak Invariance)
- Skalare Messinvarianz: Gleiche Intercepts (anderer Name: Strong Invariance)
- (Strikte Messinvarianz: Gleiche Fehlervarianzen)
- Partielle Messinvarianz: Nur teilweise Gleichheit der Ladungen oder der Intercepts
Je nach dem von Ihnen zu prüfenden Modell sind unterschiedliche Grade des Messinvarianz nötig. Für ein Cross-Lagged-Panel-Modell braucht man mindestens metrische Messinvarianz (allerdings wird zur Sicherheit teilweise auch skalare Messinvarianz empfohlen). Für Modelle, die auch die Mittelwertstruktur einschließen, wie z.B. Latent Growth Models, muss mindestens skalare Messinvarianz vorliegen.
Wenn ein nötiges Niveau der Messinvarianz nicht vorliegt, dann kann es ausreichend sein, dass lediglich partielle Messinvarianz herrscht, also im Falle der partiellen metrischen Messinvarianz, dass nicht alle Ladungen gleich sind, bzw. im Fall der partiellen skalaren Messinvarianz, dass nicht alle Intercepts gleich sind.
3. Der Beispieldatensatz
Demonstriert wird hier die Prüfung longitudinaler Messinvarianz mit einem Beispieldatensatz, der Teil von lavaan ist: PoliticalDemocracy. Dieser enthält unter anderem eine latente Variable Democracy mit vier Indikatorvariablen, die zu zwei verschiedenen Zeitpunkten gemessen wurden, 1960 und 1965. Die Variablen y1 bis y4 sind die Indikatoren des ersten Messzeitpunkts, y5 bis y8 die gleichen Indikatoren des zweiten Messzeitpunkts. (Es gehören also inhaltlich zusammen y1 und y5, y2 und y6, usw.).
Hier ist das Modell auf Basis des Datensatzes PoliticalDemocracy, wobei uns für die Messinvarianz nur die beiden latenten Variablen rechts interessieren:
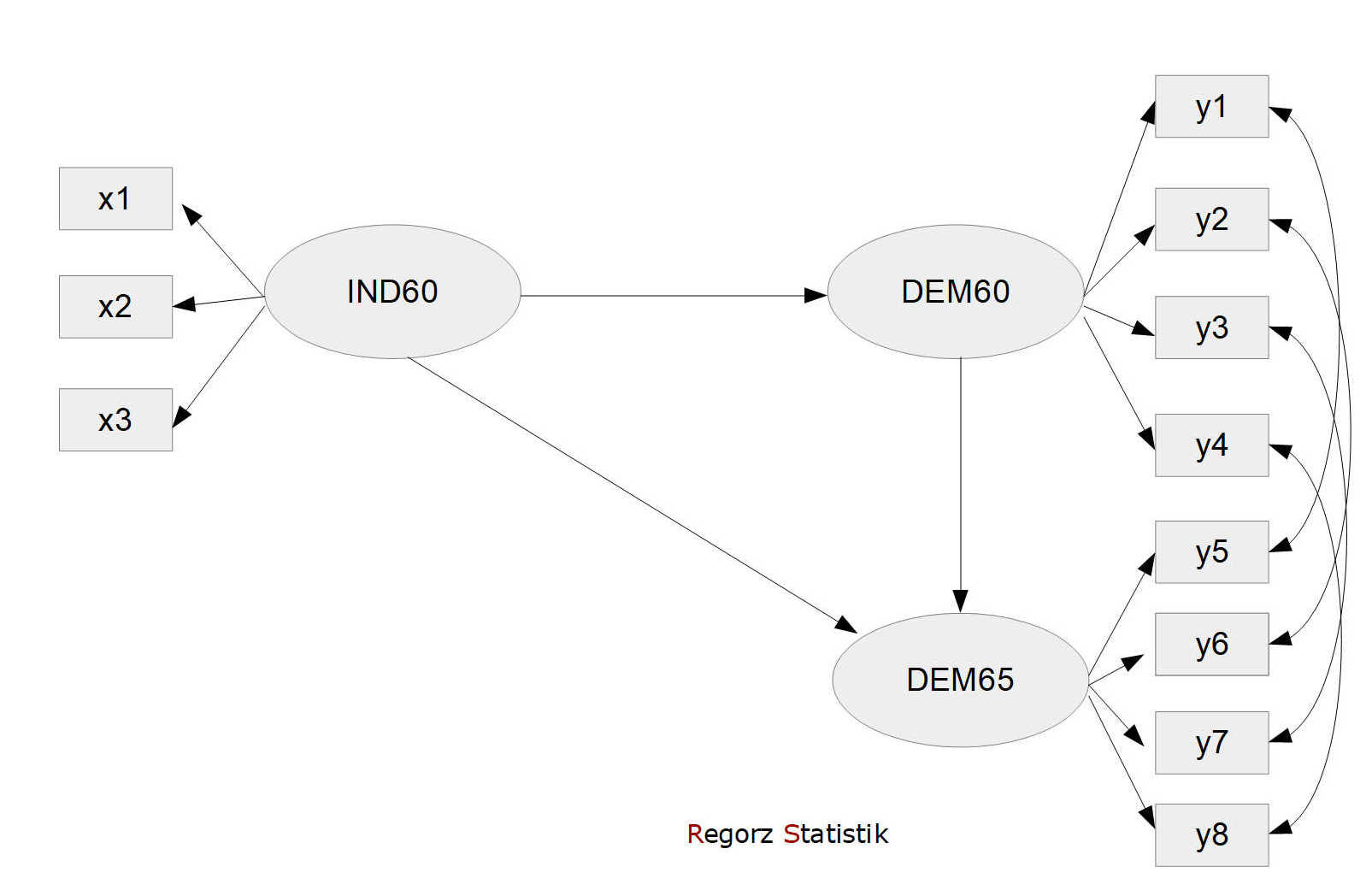
Nachfolgend wollen wir prüfen, ob die Messeigenschaften des Konstrukts Democracy über die Zeit gleich bleiben. Oder technisch ausgedrückt wollen wir prüfen, ob "the conditional distributions of observed values are unchanging given the same latent variable values over time" (Millsap & Cham, 2011, zitiert nach Newsom, 2015, S. 27). Also: Ob bei gleichen Werten der latenten Variable über die Zeit auch die zu erwartenden gemessenen Werte auf den Indikatorvariablen gleich bleiben würden.
4. Prüfung der konfiguralen Messinvarianz
Bei der konfiguralen Messinvarianz wird geprüft, ob die grundlegende Messtruktur für die verschiedenen Zeitpunkte gleich ist. Ob es also die gleichen Faktorladungen gibt (noch nicht: die gleiche Höhe der Faktorladungen) und ob es die gleichen Fehlerkovarianzen gibt (noch nicht: die gleiche Höhe der Fehlerkovarianzen). Grafisch gesprochen: Ob das Messmodell zu den verschiedenen Zeitpunkten gleich aussieht (gleiche Kästchen, Ellipsen, Pfeile), noch nicht, ob auch die gleichen Ergebnisse (z.B. Ladungen in gleicher Höhe) an den Pfeilen und Kästchen stehen.
Hier ist ein Beispielcode für die Prüfung der konfiguralen Messinvarianz; nachfolgend werden dann einige hervorgehobene Besonderheiten des Codes näher erläutert.
library(lavaan)
# Konfigurale Messinvarianz
model_config <- '
# Ladungen
dem60 =~ NA * y1 + y2 + y3 + y4
dem65 =~ NA * y5 + y6 + y7 + y8
# Varianzen und Covarianzen
dem60 ~~ 1 * dem60
dem65 ~~ 1 * dem65
dem60 ~~ dem65
y1 ~~ y5
y2 ~~ y6
y3 ~~ y7
y4 ~~ y8
# Intercepts
y1 ~ 1
y2 ~ 1
y3 ~ 1
y4 ~ 1
y5 ~ 1
y6 ~ 1
y7 ~ 1
y8 ~ 1
dem60 ~ 0 * 1
dem65 ~ 0 * 1
'
Erläuterung der hervorgehobenen Codebestandteile
Zum einen müssen in einem SEM-Modell die latenten Variablen jeweils mit einer Metrik versehen werden. Da wir bei der Messinvarianzprüfung in der Regel auch Intercepts schätzen, muss das sowohl für die Ladungen/Varianzen geschehen als auch für die Intercepts/Faktormittelwerte. Dies ist Teil des Modellierungsschritts "model identification".
Für die Metrik gibt es verschiedene Optionen. Die Default-Option in lavaan ist die Markervariable. Die Ladung des ersten Indikators einer latenten Variable wird vom System auf 1 fixiert, ebenso der erste Intercept einer latenten Variable auf 0.
Aber es gibt noch andere Möglichkeiten hierfür. Die zweite häufige ist die Fixierung der Varianz der latenten Variable auf 1 (und des Intercepts der latenten Variable auf 0). Diese Option ist m.E. für die Invarianzprüfung besser geeignet, weil man damit insbesondere eher eine partielle Messinvarianz entdecken kann (dazu weiter unten mehr). Allerdings empfiehlt es sich hier nicht, die Umstellung auf diese Identifizierungsmethode im Rahmen der Modellschätzung vorzunehmen (mit dem Parameter std.lv = TRUE), sondern dies explizit zu programmieren:
Hier wird die Schätzung der ersten Ladung freigegeben, so dass sie nicht mehr per Default auf 1 fixiert ist, indem der erste Indikator mit NA multipliziert wird:
dem60 =~ NA * y1 + y2 + y3 + y4
dem65 =~ NA * y5 + y6 + y7 + y8
Und hier wird dafür die Varianz der latenten Variablen auf 1 fixiert:
dem60 ~~ 1 * dem60
dem65 ~~ 1 * dem65
Analog wird hier der Intercept beider latenter Variablen auf 0 fixiert:
dem60 ~ 0 * 1
dem65 ~ 0 * 1
Die zweite Besonderheit sind die Fehlerterme der Items. In einem Längsschnittmodell kommen in der Regel die Items mehrfach vor, je einmal zu jedem Messzeitpunkt. In unserem Beispiel ist das Item y1 inhaltlich gleich dem Item y5, y2 gleich y6, y3 gleich y7 und y4 gleich y8 - nur jeweils zu einem anderen Zeitpunkt. Nun hat aber jedes Item neben dem Einfluss der latenten Variable, zu der es gehört, und einer Zufallsschwankung häufig auch noch eine systematische Variation, die für dieses Item spezifisch ist, die Spezifität. Wenn jetzt ein Item mehrfach, zu verschiedenen Zeitpunkten, im Datensatz vorkommt, ist zu erwarten, dass diese itemspezifische Varianz zwischen verschiedenen Messzeitpunkten miteinander zusammen hängt. Daher sollte man die Schätung der Kovarianz zulassen zwischen dem gleichen Item zu verschiedenen Zeitpunkten:
y1 ~~ y5
y2 ~~ y6
y3 ~~ y7
y4 ~~ y8
Dieses Modell kann man jetzt schätzen und den Modellfit prüfen:
fit_config <- cfa(model = model_config, data = PoliticalDemocracy)
# Globar Fit
summary(fit_config, fit.measures =TRUE, standardized =TRUE)
# Local Fit
modindices(fit_config, minimum.value = 10, sort. = TRUE)
Wenn man das mit dem Beispieldatensatz ausführt, erhält man zum Fit insbesondere folgende Ergebnisse:
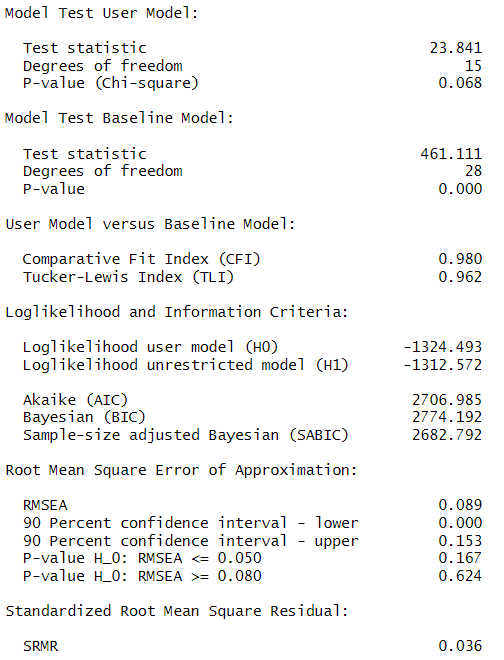
Der Modelltest ist nicht signifikant (allerdings bei einer sehr kleinen Stichprobe mit 75 Beobachtungen). CFI (.98) und SRMR (.036) sind sehr gut, lediglich der RMSEA ist etwas hoch, allerdings nicht signifikant. Insgesamt ist der globale Modellfit O.K. Beim Aufruf der Modifikationsindizes für die Prüfung des Local Fit erhält man keinen einzigen Modifikationsindex über 10 (hier nicht abgebildet). Insgesamt passt das Modell, so dass damit von konfiguraler Messinvarianz ausgegangen werden kann.
5. Prüfung der Metrischen Messinvarianz
Im nächsten Schritt prüfen wir die metrische Messinvarianz (equal loadings), also ob die Faktorladungen über die Zeit gleich bleiben. Wichtige Details sind wieder hervorgehoben.
# Metrische Messinvarianz
model_metr <- '
# Ladungen
dem60 =~ NA * y1 + l1 * y1 + l2 * y2 + l3 * y3 + l4 * y4
dem65 =~ NA * y5 + l1 * y5 + l2 * y6 + l3 * y7 + l4 * y8
# Varianzen und Covarianzen
dem60 ~~ 1 * dem60
dem65 ~~ dem65
dem60 ~~ dem65
y1 ~~ y5
y2 ~~ y6
y3 ~~ y7
y4 ~~ y8
# Intercepts
y1 ~ 1
y2 ~ 1
y3 ~ 1
y4 ~ 1
y5 ~ 1
y6 ~ 1
y7 ~ 1
y8 ~ 1
dem60 ~ 0 * 1
dem65 ~ 0 * 1
Erläuterung der hervorgehobenen Codebestandteile
In diesem Schritt führen wir Gleichheitsrestriktionen für die Ladungen ein. Die Ladung für ein bestimmtes Item und eine bestimmte latente Variable wird über die Zeit gleichgesetzt. Das erreichen wir dadurch, dass diesen Ladungen über die Zeit das gleiche Label gegeben wird. Außerdem bleibt es wie im vorherigen Schritt dabei, dass die erste Ladung abweichend vom Default frei geschätzt wird (Multiplikation mit NA). Daher kommt das jeweils erste Item eines Konstrukts zu jedem Messzeitpunkt zweimal in der Definition des jeweiligen Messmodells vor, einmal für die Gleichsetzung mit dem Label und einmal für die Freigabe mit NA:
dem60 =~ NA * y1 + l1 * y1 + l2 * y2 + l3 * y3 + l4 * y4
dem65 =~ NA * y5 + l1 * y5 + l2 * y6 + l3 * y7 + l4 * y8
Und, ganz wichtig: Jetzt ergibt sich eine Änderung bei den Faktorvarianzen. Für die konfigurale Messinvarianz wurden die Faktorvarianzen über alle Messzeitpunkte gleich 1 gesetzt. Das ist jetzt nicht mehr nötig und auch nicht mehr sinnvoll. Denn für die Modellidentifikation/Metrik reicht es, wenn zum ersten Zeitpunkt die Varianz auf 1 gesetzt wird. Damit erhalten die Ladungen zum ersten Zeitpunkt ihre Metrik und da die Ladungen zum zweiten Zeitpunkt jetzt ja die Selben sind, auch diese.
Was würde es bedeuten, wenn wir auch für spätere Messzeitpunkte die Varianzen auf 1 fixiert ließen? Damit würden wir zusätzlich zu gleichen Ladungen noch modellieren, dass die Varianzen der latenten Variablen über die Zeit gleich bleiben - aber das ist keine Frage der Messinvarianz, sondern eine inhaltliche Frage an den Datensatz. Es kann nämlich durchaus sein, dass sich Varianzen von latenten Variablen im Laufe der Zeit ändern, ohne dass das gegen die Messinvarianz spricht. Deshalb darf jetzt nur noch für den ersten Zeitpunkt die Varianz auf 1 gesetzt werden (und deshalb machen wir das hier auch manuell und eben nicht bei der Schätzung mit std.lv = TRUE):
dem60 ~~ 1 * dem60
dem65 ~~ dem65
dem60 ~~ dem65
Dieses Modell schätzen wir.
fit_metr <- cfa(model = model_metr, data = PoliticalDemocracy)
summary(fit_metr, fit.measures =TRUE, standardized =TRUE)
Anschließend prüfen wir mit dem LR-Test, ob sich der Modellfit signifikant verschlechtert hat durch die Hinzunahme der Gleichheitsrestriktion für die Ladungen. Wenn dies nicht der Fall ist, können wir die Nullhypothese, dass die Ladungen gleich sind (und damit metrische Messinvarianz herrscht), nicht verwerfen.
# LR-Test
lavTestLRT(fit_config, fit_metr)
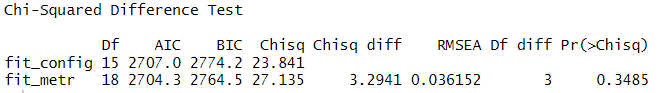
Hier wird der LR-Test nicht signifikant, so dass wir die Hypothese metrischer Messinvarianz nicht verwerfen können.
Obwohl wir vier Faktorladungen gleich gesetzt haben, weist das Modell nur drei zusätzliche Freiheitsgrade auf. Das liegt daran, dass wir jetzt zusätzlich die Varianz für den zweiten Zeitpunkt frei schätzen.
Im vorliegenden Fall ist die Stichprobe für ein SEM-Modell sehr klein. Der LR-Test ist jedoch von der Stichprobengröße abhängig und wird in größeren Stichproben leichter signifikant - bei sehr großen Stichproben u.U. schon bei trivial kleinen Abweichungen von metrischer Messinvarianz.
Daher betrachtet man häufig zusätzlich zur Signifikanz des LR-Tests auch, wie sich der Fit-Index CFI verändert.
fitMeasures(fit_metr, "cfi") - fitMeasures(fit_config, "cfi")
Im Beispiel ergibt sich als Veränderung des CFI:
cfi
-0.001
Nach Cheung und Rensvold (2002) sollte bei einer Differenz im CFI von -0.01 oder kleiner das strengere der beiden Modelle nicht verworfen werden. (Allerdings gibt es auch davon abweichende Meinungen, z.B. bei Chen, 2007, der bei Stichproben unter N = 300 eher von -0.005 als Grenze ausgeht). Hier ist die Verschlechterung im CFI deutlich kleiner als der Cut-Off-Wert, was für die metrische Messinvarianz spricht. Damit können wir bereits longitudinale SEM-Modelle schätzen, die nur auf die Beziehungen der Variablen zugreifen (und nicht auf Mittelwertsstrukturen), wie z.B. Cross-Lagged-Panel-Modelle.
Nach Newsom (2015) ist es speziell für Cross-Lagged-Panel-Modelle sinnvoll, zusätzlich noch zu prüfen, ob die Faktorvarianzen über die Zeit gleich bleiben. Denn die Pfadschätzungen in einem Cross-Lagged-Panel-Modell können durch Veränderungen in den Varianzen beeinfluss werden. Praktisch könnte man das so prüfen, dass man ein zusätzliches Modell testet, bei dem zusätzlich zu den gleichen Ladungen für alle Zeitpunkte die Faktorvarianz auf 1 festgesetzt wird. Hier also z.B. mit folgender Änderung:
dem60 ~~ 1 * dem60
dem65 ~~ 1* dem65
dem60 ~~ dem65
Auf die Durchführung dieses Schritts wird im vorliegenden Beispiel verzichtet.
6. Prüfung der Skalaren Messinvarianz
Nachdem wir metrische Messinvarianz gezeigt haben, prüfen wir als nächstes skalare Messinvarianz. Dazu werden zusätzlich die Item-Intercepts über die verschiedenen Messzeitpunkte gleich gesetzt. Wichtige Elemente des Codes sind wieder hervorgehoben.
model_skal <- '
# Ladungen
dem60 =~ NA * y1 + l1 * y1 + l2 * y2 + l3 * y3 + l4 * y4
dem65 =~ NA * y5 + l1 * y5 + l2 * y6 + l3 * y7 + l4 * y8
# Varianzen und Covarianzen
dem60 ~~ 1 * dem60
dem65 ~~ dem65
dem60 ~~ dem65
y1 ~~ y5
y2 ~~ y6
y3 ~~ y7
y4 ~~ y8
# Intercepts
y1 ~ i1 * 1
y2 ~ i2 * 1
y3 ~ i3 * 1
y4 ~ i4 * 1
y5 ~ i1 * 1
y6 ~ i2 * 1
y7 ~ i3 * 1
y8 ~ i4 * 1
dem60 ~ 0 * 1
dem65 ~ 1
'
Erläuterung der hervorgehobenen Codebestandteile
Die Intercepts werden über die Zeit gleichgesetzt, indem verschiedene Intercepts für das inhaltich gleiche Item dasselbe Label zugewiesen bekommen.
y1 ~ i1 * 1
y2 ~ i2 * 1
y3 ~ i3 * 1
y4 ~ i4 * 1
y5 ~ i1 * 1
y6 ~ i2 * 1
y7 ~ i3 * 1
y8 ~ i4 * 1
Und analog zum Vorgehen bei der Fixierung der Varianz wird jetzt auch bei den Faktorintercepts nur noch der erste Intercept auf 0 fixiert zur Modellidentifizierung, die nachfolgenden werden frei geschätzt. Denn wenn wir weiterhin alle Faktorintercepts auf 0 fixieren würden, würden wir zusätzlich auch prüfen, ob sich die latenten Variablen über die Zeit nicht im Mittelwert ändern - das ist aber wiederum keine Frage der Messinvarianz, sondern eine inhaltliche Frage zu den Daten.
dem60 ~ 0 * 1
dem65 ~ 1
Dieses Modell schätzen wir und führen anschließend den LR-Test im Vergleich zum vorherigen Modell durch.
fit_skal <- cfa(model = model_skal, data = PoliticalDemocracy) summary(fit_skal, fit.measures =TRUE, standardized =TRUE)
# LR-Test
lavTestLRT(fit_metr, fit_skal)

Der LR-Test ist nicht signifikant, so dass wir die Hypothese skalarer Messinvarianz nicht verwerfen können. Zusätzlich betrachten wir noch die Veränderung im CFI.
fitMeasures(fit_skal, "cfi") - fitMeasures(fit_metr, "cfi")
cfi
-0.007
Die Veränderung des CFI liegt unter -0.01, so dass auch dieses Maß für skalare Messinvarianz spricht. Damit können wir auch longitudinale SEM-Modelle schätzen, die auf Mittelwertsstrukturen zugreifen.
7. Prüfung der Strikten Messinvarianz
Manchmal findet man noch das Konzept einer strikten Messinvarianz, bei der zusätzlich noch die Fehlervarianzen der Items über die Zeit gleich gesetzt werden. Allerdings ist das eine sehr restriktive Annahme, und ich habe in der Literatur noch keinen wirklich plausiblen Grund gefunden, warum man das überhaupt prüfen sollte - für longitudinale SEM-Modelle ist es nach meinem Kenntnisstand nicht erforderlich. Falls Ihr Prüfer das aber von Ihnen verlangt, ist nachfolgend unkommentiert ein entsprechendes Codebeispiel abgedruckt. Die Änderung zum vorherigen Schritt ist einfach, dass jetzt auch die Varianzen der Items über die Messzeitpunkte hinweg gleich gesetzt werden.
model_strikt <- '
# Ladungen
dem60 =~ NA * y1 + l1 * y1 + l2 * y2 + l3 * y3 + l4 * y4
dem65 =~ NA * y5 + l1 * y5 + l2 * y6 + l3 * y7 + l4 * y8
# Varianzen und Covarianzen
dem60 ~~ 1 * dem60
dem65 ~~ dem65
dem60 ~~ dem65
y1 ~~ y5
y2 ~~ y6
y3 ~~ y7
y4 ~~ y8
y1 ~~ v1 * y1
y2 ~~ v2 * y2
y3 ~~ v3 * y3
y4 ~~ v4 * y4
y5 ~~ v1 * y5
y6 ~~ v2 * y6
y7 ~~ v3 * y7
y8 ~~ v4 * y8
# Intercepts
y1 ~ i1 * 1
y2 ~ i2 * 1
y3 ~ i3 * 1
y4 ~ i4 * 1
y5 ~ i1 * 1
y6 ~ i2 * 1
y7 ~ i3 * 1
y8 ~ i4 * 1
dem60 ~ 0 * 1
dem65 ~ 1
'
fit_strikt <- cfa(model = model_strikt, data = PoliticalDemocracy)
summary(fit_strikt, fit.measures =TRUE, standardized =TRUE)
lavTestLRT(fit_skal, fit_strikt)
fitMeasures(fit_strikt, "cfi") - fitMeasures(fit_skal, "cfi")
8. Literatur
Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling, 14(3), 464–504.
Cheung, G. W., & Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling, 9(2), 233-255.
Little, T. D. (2013). Longitudinal structural equation modeling. Guilford press.
Little, T. D., Preacher, K. J., Selig, J. P., & Card, N. A. (2007). New developments in latent variable panel analyses of longitudinal data. International Journal of Behavioral Development, 31(4), 357-365.
Newsom, J. T. (2015). Longitudinal structural equation modeling: A comprehensive introduction. Routledge.