Strukturgleichungsmodelle mit R lavaan
3. Moderationsanalyse - latente Interaktionen

Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, 24.04.2023

Dieses Tutorial zeigt die Prüfung einer latenten Interaktion mit dem Verfahren des Double Mean Centering (SEM Moderationsanalyse).

Video

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

Grundlagen der latenten Moderation mit Double Mean Centering

Wenn man mit einem vollen SEM-Modell (mit latenten Variablen) eine Moderationsanalyse durchführen möchte, stellt sich vor allem eine Herausforderung: Wie modelliert man eine latente Interaktionsvariable? Aus der moderierten Regression kennt man das Vorgehen, dass man eine Moderation prüft, indem man UV, Moderator und Interaktion UV-Moderator in eine multiple Regression einschließt. Im Strukturgleichungsmodell funktioniert das grundsätzlich genauso, nur muss man irgendwie Indikatorvariablen für die dann latente Interaktion ermitteln. Hierfür gibt es verschiedene Verfahren, die in der Literatur diskutiert werden.

Das Modellieren latenter Interaktionen (Moderationsanalyse) in einem Strukturgleichungsmodell (SEM) kann u.a. mithilfe der Double Mean Centering Methode durchgeführt werden. Diese Methode ermöglicht es, die Interaktionseffekte von moderierenden Variablen auf die Beziehung zwischen einer unabhängigen und abhängigen Variable zu analysieren. Hier sind die dafür nötigen Schritte:

Schritt 1: Zentrierung der Indikatorvariablen
Um die Double Mean Centering Methode anzuwenden, ist es in einem ersten Schritt wichtig, die Indikatorvariablen, die in das SEM-Modell aufgenommen werden, zu zentrieren. Zentrierung bedeutet, dass der Durchschnitt der Variablen auf Null gesetzt wird, indem von jedem Datenpunkt der Durchschnitt der jeweiligen Variablen über alle Beobachtungen abgezogen wird.

Schritt 2: Bildung der Interaktionsterme
Nachdem die Indikatorvariablen zentriert wurden, können die Interaktionsterme erstellt werden. Dies erfolgt durch die Multiplikation der zentrierten Werte des Moderators mit den zentrierten Werten der unabhängige Variable.

Schritt 3: Zentrierung der Interaktionsterme
Nach der Bildung der Interaktionsterme ist es wichtig, auch diese nochmals zu zentrieren (daher Double Mean Centering).

Schritt 4: Einbau der Interaktionsterme ins SEM-Modell
Nachdem die Interaktionsterme zentriert wurden, können sie in das SEM-Modell eingeführt werden, indem sie als Indikatoren für eine latente Interaktionsvariable verwendet werden.

Schritt 5: Berücksichtigung von Fehlerkovarianzen
Für die Schätzung eines solchen Modells ist zu berücksichtigen, dass mehrere der (doppelt zentrierten) Interaktionsindikatoren miteinander Gemeinsamkeiten haben. So teilt beispielsweise (in einem Modell mit je drei Indikatoren für UV und Moderator) die Interaktionsvariable IV1-MOD1 eine Komponente mit den Interaktionen IV1-MOD2 und IV1-MOD3, sowie auch mit IV2-MOD1 und IV3-MOD1. Aus diesem Grund ist zu erwarten, dass auch ihr Fehlerterm mit den Fehlertermen dieser anderen (hier: vier) Variablen korreliert ist.

Hier ist ein relevantes Paper, wenn Sie die Methode des Double Mean Centering anwenden möchten:
Lin, G. C., Wen, Z., Marsh, H. W., & Lin, H. S. (2010). Structural equation models of latent interactions: Clarification of orthogonalizing and double-mean-centering strategies. Structural Equation Modeling, 17(3), 374-391.

R-Code für Double Mean Centering

Neben lavaan benötigen wir noch semTools, das uns das Double Mean Centering abnimmt (wobei man das natürlich auch "per Hand" selbst programmieren könnte - das wird weiter unten auf der Seite demonstriert.).

library(lavaan)
library(semTools)

head(mydata)

Den Modell-Fit sollte man testen, bevor man die latente Interaktion eingefügt haben:

# Fit testen (noch ohne Interaktion)

# Messmodell (step 1)

test_model <- '
# Ladungen
iv =~ IV1 + IV2 + IV3
mod =~ MOD1 + MOD2 + MOD3
dv =~ DV1 + DV2 + DV3
'

test_fit <- cfa(test_model, data = mydata, estimator="MLM")

summary(test_fit, fit.measures = TRUE, standardized=TRUE)

mi <- modificationindices(test_fit)
mi[mi$mi>10,]

# Strukturmodell (step 2; hier nicht nötig, da saturiert)

test_model2 <- '
# Ladungen
iv =~ IV1 + IV2 + IV3
mod =~ MOD1 + MOD2 + MOD3
dv =~ DV1 + DV2 + DV3

dv ~ iv + mod
'

test_fit2 <- sem(test_model2, data = mydata, estimator="MLM")

summary(test_fit2, fit.measures = TRUE, standardized=TRUE)

mi <- modificationindices(test_fit)
mi[mi$mi>10,]

Wenn wir einen akzeptablen Modell-Fit für unser Modell erzielt haben, können wir jetzt die Modellierung der latenten Interaktion in das Modell einfügen.

# Double Mean Centering

Die indProd()-Funktion übernimmt dabei die doppelte Zentrierung. Wir übergeben den Data-Frame und zwei Listen mit den Indikatorvariablen, die wir für die Interaktionsterme verwenden wollen. Und wir müssen sowohl meanC als auch doubleMC auf TRUE setzen.

mydata_dmc <- indProd (mydata , var1 = c("IV1", "IV2", "IV3"),
var2 = c("MOD1", "MOD2", "MOD3"),
match = FALSE , meanC = TRUE ,
residualC = FALSE , doubleMC = TRUE)

head(mydata_dmc)

Bei der Modellschätzung werden jetzt alle so erzeugten doppelt zentrierten Indikatorvariablen für das Messmodell der latenten Interaktion angegeben. Der mit Abstand fehlerträchtigste Schritt ist das Spezifizieren der Fehlerkovarianzen, bei der jeweils Kovarianzen zwischen den Interaktionsindikatoren zugelassen werden müssen, die ein gemeinsames Element haben. Hier lohnt es sich, das zwei- oder dreimal zu prüfen - ein einziger Fehler hier kann den Modellfit massiv verschlechtern.

# Modellschätzung mit latenter Interaktion

int_model <- '
# Ladungen
iv =~ IV1 + IV2 + IV3
mod =~ MOD1 + MOD2 + MOD3
dv =~ DV1 + DV2 + DV3
int =~ IV1.MOD1 + IV1.MOD2 + IV1.MOD3 + IV2.MOD1 + IV2.MOD2 +
IV2.MOD3 + IV3.MOD1 + IV3.MOD2 + IV3.MOD3

# Regression
dv ~ iv + mod + int

# Fehlerkovarianzen
IV1.MOD1 ~~ IV1.MOD2 + IV1.MOD3 + IV2.MOD1 + IV3.MOD1
IV1.MOD2 ~~ IV1.MOD3 + IV2.MOD2 + IV3.MOD2
IV1.MOD3 ~~ IV2.MOD3 + IV3.MOD3
IV2.MOD1 ~~ IV2.MOD2 + IV2.MOD3 + IV3.MOD1
IV2.MOD2 ~~ IV2.MOD3 + IV3.MOD2
IV2.MOD3 ~~ IV3.MOD3
IV3.MOD1 ~~ IV3.MOD2 + IV3.MOD3
IV3.MOD2 ~~ IV3.MOD3
'

int_fit <- sem(int_model, data = mydata_dmc, estimator="MLM")

summary(int_fit, fit.measures = TRUE, standardized=TRUE)

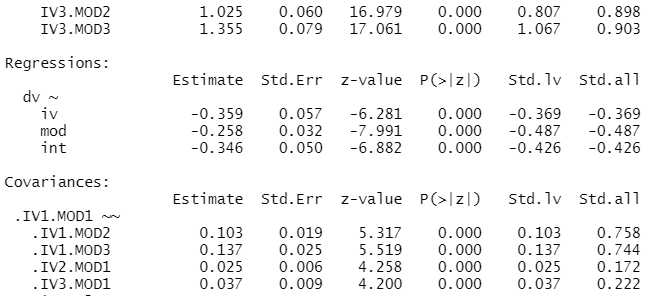
Hier sehen wir, dass die latente Interaktion (Pfad dv ~ int) signifikant ist, wir haben also einen Moderationseffekt zeigen können.

Wenn man bei signifikanter (latenter) Interaktion ähnlich wie bei der Regression jetzt Simple Slopes betrachten möchte, kann man diese über die beiden Funktionen probe2WayMC() und plotProbe() anfordern.

# Simple Slopes

probe <- probe2WayMC(int_fit, c("iv", "mod", "int"), "dv", "mod",
c(-sqrt(1.462),0, sqrt(1.462)))
probe

Die Werte in der Liste, -sqrt(1.462) usw., sollen hier -1 SD, 0 und +1 SD angeben. Dazu habe ich im Modelloutput nachgesehen, wie hoch die geschätzte Varianz des Moderators ist. Dort wurde ein Wert von 1.462 angegeben. Damit ist dann die Wurzel (sqrt) dieses Wertes die Standardabweichung des Moderators.

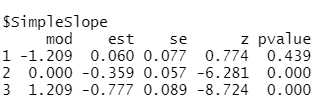
plotProbe(probe, c(-3,3))

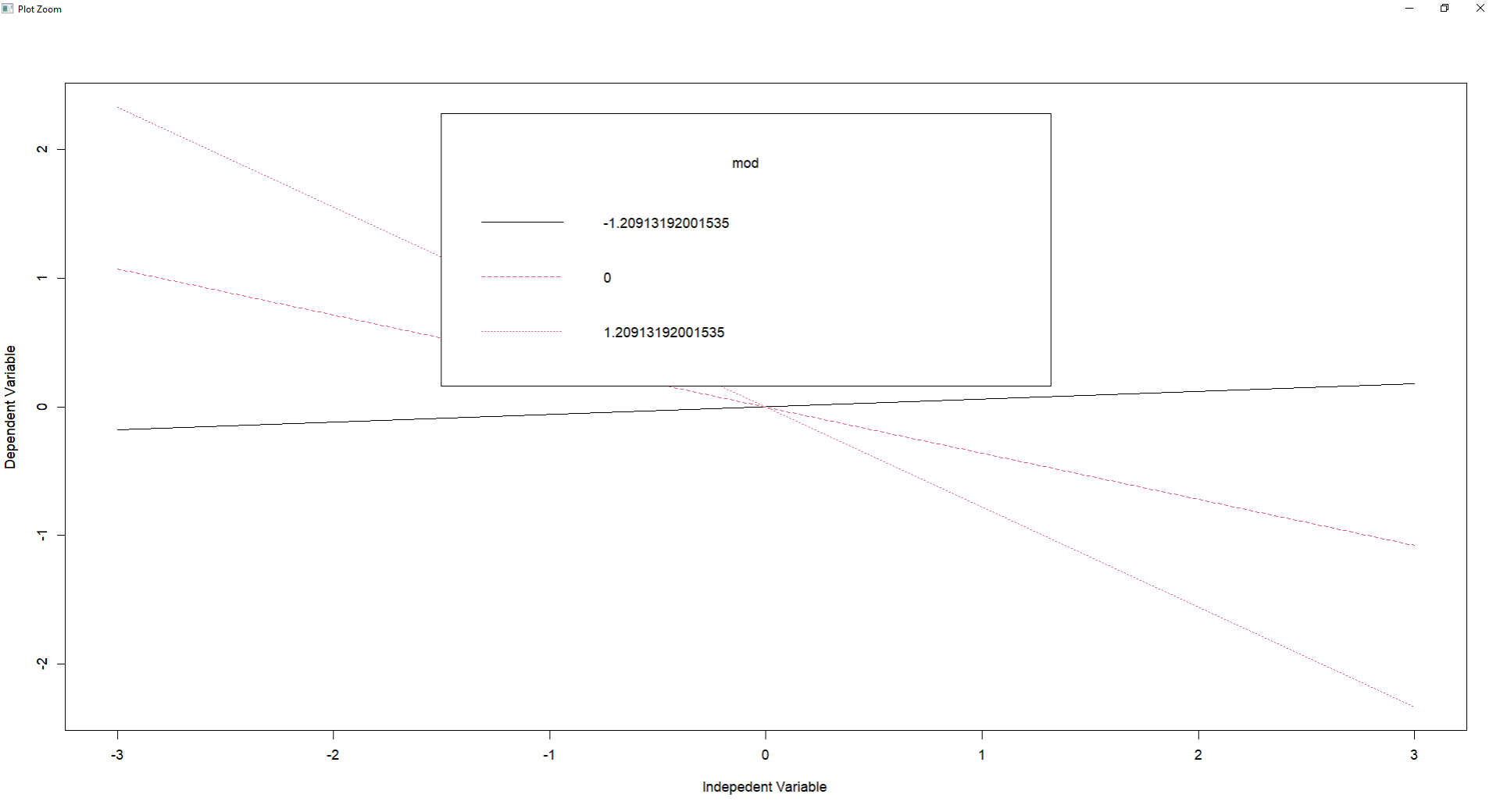
Manueller R-Code für Double Mean Centering
(statt mit der indProd-Funktion)

Zur Illustration ist hier die doppelte Zentrierung statt mit der o.g. Funktion per Hand programmiert. Vielleicht wird damit das Vorgehen beim Double Mean Centering deutlicher.

# Double mean centering per Hand

mydata2 <- latent_interaction_SEM_full

# Step 1: Mean Centering der Indikatoren (1. Mean Centering)

attach(mydata2)
mydata2$IV1c <- scale(IV1, scale = FALSE)
mydata2$IV2c <- scale(IV2, scale = FALSE)
mydata2$IV3c <- scale(IV3, scale = FALSE)
mydata2$MOD1c <- scale(MOD1, scale = FALSE)
mydata2$MOD2c <- scale(MOD2, scale = FALSE)
mydata2$MOD3c <- scale(MOD3, scale = FALSE)
detach(mydata2)

# Step 2: Produktvariablen

attach(mydata2)
mydata2$I1M1 <- IV1c * MOD1c
mydata2$I1M2 <- IV1c * MOD2c
mydata2$I1M3 <- IV1c * MOD3c
mydata2$I2M1 <- IV2c * MOD1c
mydata2$I2M2 <- IV2c * MOD2c
mydata2$I2M3 <- IV2c * MOD3c
mydata2$I3M1 <- IV3c * MOD1c
mydata2$I3M2 <- IV3c * MOD2c
mydata2$I3M3 <- IV3c * MOD3c
detach(mydata2)

# Step 3: Mean Centering der Produktvariablen (2. Mean Centering)

attach(mydata2)
mydata2$I1M1c <- scale(I1M1, scale = FALSE)
mydata2$I1M2c <- scale(I1M2, scale = FALSE)
mydata2$I1M3c <- scale(I1M3, scale = FALSE)
mydata2$I2M1c <- scale(I2M1, scale = FALSE)
mydata2$I2M2c <- scale(I2M2, scale = FALSE)
mydata2$I2M3c <- scale(I2M3, scale = FALSE)
mydata2$I3M1c <- scale(I3M1, scale = FALSE)
mydata2$I3M2c <- scale(I3M2, scale = FALSE)
mydata2$I3M3c <- scale(I3M3, scale = FALSE)
detach(mydata2)

head(mydata2)