Äquivalenztest – Test auf Abwesenheit eines Effekts
Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, Stand: 19.11.2020
Häufig möchte man prüfen, ob es keinen Effekt gibt. Also, dass zwei Gruppen sich nicht hinsichtlich einer abhängigen Variable unterscheiden. Oder, dass zwei Variablen keinen linearen Zusammenhang (Korrelation) aufweisen.
Einen Effekt auf exakte Gleichheit zu Null zu testen, ist leider nicht möglich. Aber man kann testen, ob ein Effekt so klein ist, dass man ihn als annähernd Null ansehen kann. Dafür gibt es das Instrument des Äquivalenztests, das nachfolgend vorgestellt werden soll.
Inhalt
- Warum Äquivalenztest?
- Wie darf man es nicht prüfen?
- Grundidee Äquivalenztest
- TOST-Ansatz
- 90%-Konfidenzintervall als Alternative zu TOST
- SESOI (smallest effect size of interest)
- Umsetzung mit SPSS, jamovi und R
- Äquivalenztest gegen anderen Wert als Null
- Quellen
1. Warum Äquivalenztest?
In der Forschungspraxis trifft man häufiger auf die Frage, ob ein Effekt gleich Null ist. Beispielsweise besagt eine Theorie, dass zwischen Gruppe A und Gruppe B kein Unterschied für eine bestimmte abhängige Variable besteht. Oder eine Theorie besagt, dass es zwischen Merkmal C und Merkmal D keinen Zusammenhang gibt. Wenn man diese Theorien prüfen möchte, braucht man einen Weg, um die Abwesenheit eines Effektes zu testen. Das ist konzeptionell jedoch gar nicht so einfach.
2. Wie darf man es nicht prüfen?
Mitunter sieht man, dass aus einem nicht signifikanten Ergebnis bei einem klassischen Hypothesentest geschlossen wird, dass es keinen Effekt gibt.
Z.B. wird aus einem nicht signifikanten t-Test auf unabhängige Stichproben geschlossen, dass beide Gruppen gleich sind. Oder aus einem nicht signifikanten Test für eine Korrelation wird geschlossen, dass es zwischen beiden Variablen keinen Zusammenhang gibt. Das beruht jedoch auf einem grundlegend falschen Verständnis von Hypothesentests.
Wenn das Ergebnis eines Tests nicht signifikant ist, hat man lediglich keinen Beleg für einen Effekt gefunden (absence of proof). Man hat damit keinen Beleg dafür gefunden, dass es keinen Effekt gibt (proof of absence).
Wenn man mit den normalen Hypothesentests die Abwesenheit eines Effekts nicht prüfen kann, gibt es dann vielleicht Spezialtests, mit denen man zeigen kann, dass der Mittelwertsunterschied zwischen zwei Gruppen gleich Null ist, oder mit denen man zeigen kann, dass die Korrelation zwischen zwei Merkmalen Null ist?
Im engeren Sinne leider nicht. Man kann für ein kontinuierliches Merkmal statistisch nicht den Beleg erbringen, dass ein Effekt genau gleich Null ist. Das kann man am Beispiel eines Mittelwertsunterschieds gut verdeutlichen:
Beim klassischen Hypothesentest konstruiert man einen Ablehnungsbereich. Wenn der tatsächlich gemessene Mittelwertsunterschied in diesen Bereich fällt, lehnt man die Nullhypothese ab, dass beide Gruppen gleich sind – und zeigt damit, dass sie ungleich sind.
Wenn der tatsächliche Mittelwertsunterschied in der Stichprobe so groß ist, dass er in den Ablehnungsbereich fällt (also bei einem großen positiven oder negativen Mittelwertsunterschied), dann ist das bei tatsächlicher Mittelwertsgleichheit in der Grundgesamtheit sehr unwahrscheinlich (bei alpha = .05 ist die Wahrscheinlichkeit dann kleiner als 5%). Und dann wird die Nullhypothese einer Mittelwertsgleichheit abgelehnt, so dass man von einem Mittelwertsunterschied ausgeht.
Wenn wir jetzt aber keinen Mittelwertsunterschied zeigen wollen, sondern eine Mittelwertsgleichheit, dann müssten wir H0 und H1 umdrehen. Unsere H0 wäre dann, dass sich die Mittelwerte unterscheiden und die H1, dass die Mittelwerte gleich sind. Aber es lassen sich leider keine Ablehnungsbereiche konstruieren, die dazu führen, dass wir unsere neue H1 verwerfen können, denn:
Wenn tatsächlich ein, auch nur minimaler, Mittelwertsunterschied vorliegt (z.B. d = 0.0001), kann man die H0 eines Mittelwertsunterschieds nicht ablehnen. Denn es liegt dann in der Stichprobe ja ein Mittelwertsunterschied vor. Und selbst wenn in der Stichprobe sich ein Mittelwertsunterschied von exakt Null zeigt (z.B. d = 0.0000), können wir nicht mit hinreichender Wahrscheinlichkeit davon ausgehen, dass auch der wahre Wert in der Grundgesamtheit gleich Null ist – er könnte ja auch minimal positiv oder minimal negativ sein, das Stichprobenergebnis ist fast nie exakt gleich dem wahren Wert in der Grundgesamtheit. Es gibt also kein mögliches Ergebnis beim Stichprobentest, das ein hinreichender Beleg für das Verwerfen der H0 eines Mittelwertsunterschieds (und damit das Bestätigen einer Mittelwertsgleichheit) wäre.
3. Grundidee Äquivalenztest
Wie kann man dieses Problem jetzt lösen? Die Grundidee eines Äquivalenztests ist folgende: Man testet nicht mehr, ob ein Effekt exakt gleich Null ist. Sondern man testet, ob der Effekt so klein ist, dass er hinreichend nahe bei Null ist. Wie nahe bei Null da hinreichend ist, hängt von der Fragestellung ab, darauf werden wir weiter unten unter SESOI (smallest effect size of interst) noch weiter eingehen.
Es werden also beim Äquivalenztest zwei Grenzen für den Effekt festgelegt: eine obere Grenze und eine untere Grenze. Und dann wird mit geeigneten Verfahren (siehe nächste zwei Abschnitte) geprüft, ob der Effekt signifikant kleiner als die Obergrenze des Effekts ist und gleichzeitig signifikant kleiner als die Untergrenze des Effekts. Wenn beide Bedingungen erfüllt sind, sprechen wir von einem Effekt, der äquivalent zu Null ist.
Zur Prüfung gibt es zwei eng miteinander verwandte Ansätze: den TOST-Ansatz (two one sided tests) und das 90%-Konfidenzintervall.
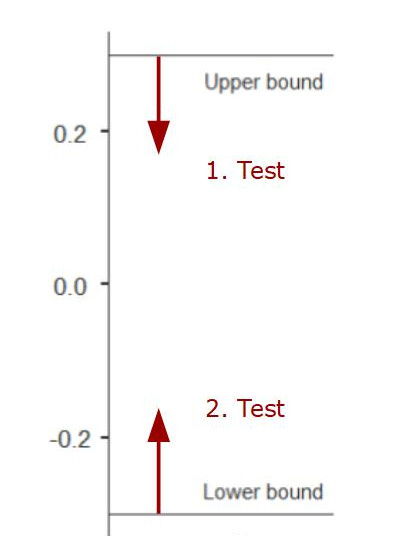
4. TOST-Ansatz
Beim two one-sided tests (oder auch two one-tailed tests) Ansatz wird die Äquivalenz durch zwei einseitige Tests bestimmt. Es wird im ersten (einseitigen) Test getestet, ob der Effekt kleiner als eine vorher festgelegte Obergrenze ist. Und im zweiten (einseitigen) Test wird getestet, ob der Effekt größer als eine vorher festgelegte Untergrenze ist. Wenn beide Tests signifikant werden, dann weiß man, dass der Effekt zwischen diesen beiden Grenzen liegt, und damit äquivalent zu Null ist.
5. 90%-Konfidenzintervall als Alternative zu TOST
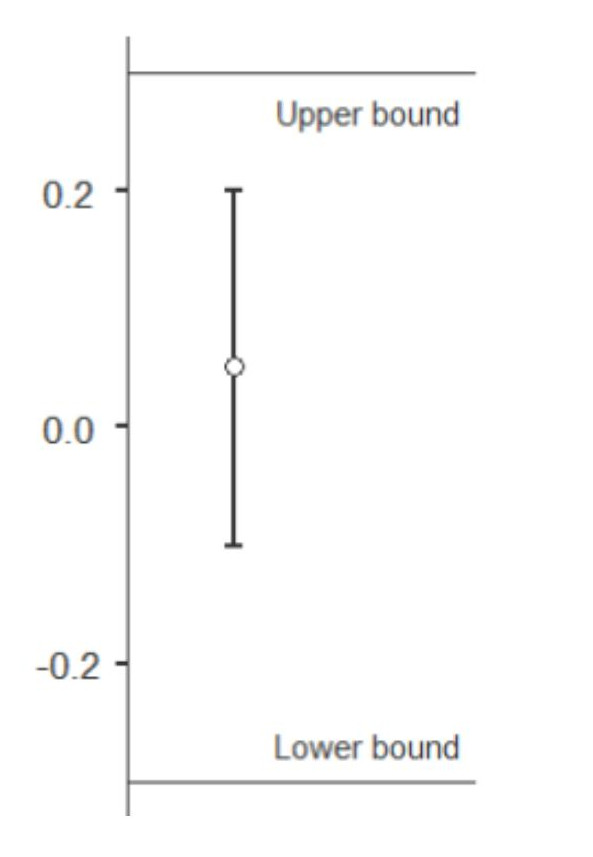
Generell kann man statt mit Hypothesentests zu den exakt gleichen Ergebnissen auch über Konfidenzintervalle kommen. Um mit einem Konfidenzintervall den o.g. TOST-Ansatz nachzubauen, muss man ein 90%-Konfidenzintervall konstruieren – dieses entspricht genau zwei einseitigen Tests mit alpha = .05.
Wenn dieses Konfidenzintervall vollständig innerhalb der vorher festgelegten Grenzen für die Äquivalenz liegt (also die Obergrenze des Konfidenzintervalls kleiner ist als die obere Äquivalenzgrenze und die Untergrenze des Konfidenzintervalls gleichzeitig größer ist als die untere Äquivalenzgrenze), dann ist Äquivalenz gezeigt.
6. SESOI (smallest effect size of interest)
Die wichtigste inhaltliche Entscheidung, wenn man einen Äquivalenztest durchführen will, ist die Bestimmung der Grenzen für Äquivalenz: Bis zu welchem z.B. Gruppenunterschied geht man noch von einer Äquivalenz aus und von welchem Wert an nicht mehr? Mit anderen Worten: Was ist der kleinste Effekt, der noch so groß ist, dass er theoretisch oder praktisch relevant ist (smallest effect size of interest – SESOI)?
Eine SESOI kann nach Lakens, Scheel, and Isager (2018) objektiv oder subjektiv bestimmt werden: Eine objektive Bestimmung sollte auf einer quantifizierbaren, theoriebasierten Vorhersage beruhen. Ein Beispiel dafür wäre, dass ein Effekt bemerkbar ist. Wenn z.B. Patienten eine Veränderung ihres psychischen Zustands (gemessen mit irgendeinem Messinstrument, z.B. einem Fragebogen) erst ab einem bestimmten Effekt überhaupt selbst als Verbesserung bemerken, wäre dies eine mögliche objektive SESOI. Für eine subjektive Bestimmung gibt es verschiedene Möglichkeiten: Verwendung eines Benchmarks (z.B. Cohen's Charakterisierungen von schwachen, mittleren und großen Effekten), Verwendung von Effektstärken aus der Literatur zum eigenen Untersuchungsthema oder eine Festlegung auf Basis der eigenen Forschungsressourcen.
Eine ausführliche Darstellung dieser Möglichkeiten zur Bestimmung einer SESOI findet sich bei Lakens, Scheel, and Isager (2018). Wichtig ist dabei, dass die SESOI und damit die Grenzen für den Äquivalenztest bestimmt werden vor Beginn der Datenerhebung.
7. Umsetzung mit SPSS, jamovi und R
Die aktuell wohl einfachste Möglichkeit, einen Äquivalenztest durchzuführen, wäre die freie Statistik-Software jamovi. Dort gibt es ein Zusatzmodul für die Durchführung von Äquivalenztests, TOSTER. Dieses enthält Äquivalenztests für:
- t-Test für unabhängige Stichproben
- t-Test für abhängige Stichproben
- Einstichproben t-Test
- Korrelation
- Vergleich zweier Anteile
Für die beiden m.E. wichtigsten Tests, t-Test für unabhängige Stichproben und Korrelationen habe ich je ein (englischsprachiges) Tutorial erstellt:
(Hinweis: Mit Anklicken der Videos wird ein Angebot des Anbieters YouTube genutzt.)
Für die Umsetzung mit R gibt es die TOSTER Package, auf der auch das o.g. jamovi-Modul beruht. Am einfachsten lässt sich der R-Code mit jamovi schreiben (jamovi kann für Auswertungen gleichzeitig den dazu gehörigen R Code exportieren, da jamovi auf R basiert). Wie man mit jamovi zu R-Code kommt, ist ebenfalls in den beiden o.g. Videos erläutert.
Man auch mit SPSS Äquivalenztests durchführen, allerdings muss man da einige Umwege gehen.
Für den Vergleich zweier Gruppen nimmt man einen online-Effektstärkenrechner zur Hilfe zur Konstruktion eines 90%-Konfidenzintervalls für d, das ist hier (auf englisch) erklärt:
(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)
Und für die Testung, ob eine Korrelation äquivalent zu Null ist, benötigt man SPSS-Syntax, um ein 90% Konfidenzintervall für r zu berechnen, das ist hier (auf englisch) erklärt:
(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)
8. Äquivalenztest gegen anderen Wert als Null
In den o.g. Beispielen ging es darum zu zeigen, dass ein Effekt (z.B. Mittelwertsunterschied, Korrelation) äquivalent zu Null ist. Das ist aber nicht das einzige mögliche Einsatzgebiet für Äquivalenztests. Man kann, durch eine andere Wahl der Äquivalenzgrenzen, auch testen, ob der Effekt äquivalent zu einem konkreten Wert ist.
Wenn man z.B. aus der Literatur weiß, dass ein bestimmter Effekt ca. bei r = .40 liegt, kann man mit einem Äquivalenztest prüfen, ob (z.B. mit einem anderen Messinstrument) die Korrelation äquivalent zu diesem Wert ist, indem man die Grenzen für Äquivalenz nicht um r = .00 sondern um r = .40 legt.
9. Quellen
Lakens, D. (2017). Equivalence tests: a practical primer for t tests, correlations, and meta-analyses. Social psychological and personality science, 8, 355-362. https://doi.org/10.1177/1948550617697177
Lakens, D., Scheel, A. M., & Isager, P. M. (2018). Equivalence testing for psychological research: A tutorial. Advances in Methods and Practices in Psychological Science, 1, 259-269. https://doi.org/10.1177/2515245918770963
Schuirmann, D. J. (1987). A comparison of the two one-sided tests procedure and the power approach for assessing the equivalence of average bioavailability. Journal of pharmacokinetics and biopharmaceutics, 15, 657-680. https://doi.org/10.1007/BF01068419