R - Mediation Analysis with PROCESS Model 4
Running Hayes' PROCESS-macro (Version 3.5 and later) with R
Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, 04/06/2021
For years the PROCESS macro has been the standard way of testing indirect effects when using SPSS. At the end of 2020 Hayes has released the PROCESS function for R, too. This tutorials will show you how to run and interpret a mediation analysis with Hayes' PROCESS function for R / RStudio.
Content
- Video tutorial
- Downloading PROCESS
- Initializing the Code
- Testing a Mediation Model
- Sample Output 1 – Simple Mediation
- Additional Parameters
- My Favorite Mediation R-Code
- Sample Output 2 – Mediation with Additional Options
- Parallel Mediation
- Parallel Mediation R-Code
- Sample Output 3 – Parallel Mediation
- More Information
1. Video tutorial
(Note: When you click on this video you are using a service offered by YouTube.)
2. Downloading PROCESS
You can download PROCESS for R from here:
https://www.processmacro.org/download.html
Currently (February, 2021) you will find a folder named “PROCESS v3.5beta for R”. There you will find an R-file “process.r”. Please be aware that it is at this point in time still a beta version so there could be bugs in the code.
3. Initializing the Code
Since PROCESS is not an R package you cannot use the commands install.packages() and library() with it. As a user defined function it has to be installed by running the file “process.r”.
If you open it in Rstudio, run it. It will take a minute or two for the code to run. After that has been completed you have gained a new R function, process(). With this function you can run PROCESS in the R environment in your active R session.
If you do not want to have to rerun the code of process.r each time you open R then Hayes recommends saving your R workspace after running process.r
4. Testing a Mediation Model
The simplest R/PROCESS code for a mediation model would be this:
process (data = my_data_frame, y = "my_DV", x = "my_IV", m ="my_mediator", model = 4)
In this example code I have used the following variable names you should replace with the names of your data:
- my_data_frame: My data frame with the data I want to use to test a mediation
- my_DV: The name of the dependent variable in my data frame
- my_IV: The name of the independent variable in my data frame
- my_mediator: The name of the mediator variable in my data frame
For the variables there are some important things to consider:
- The variable names must be put into quotation signs.
- Variable names in R are case sensitive (upper case, lower case).
- In the case of a binary variable it is not allowed to be a factor variable – you have to transform it into a numeric variable before using it with PROCESS.
And the function process has to be written in lower case letters.
5. Sample Output 1 – Simple Mediation
Here is an example of the output you could get with that code:

(A): The a-path of the mediation (IV->MED). It is significant, because p < .05
Coeff: unstandardized regression coefficient b.
LLCI and ULCI: Limits of a CI for b based on a normality assumption.
(B): The c'-path (direct effect) of the mediation (IV->DV). It is not significant, because p > .05
(C): The b-path of the mediation (MED->DV); significant, because p < .05
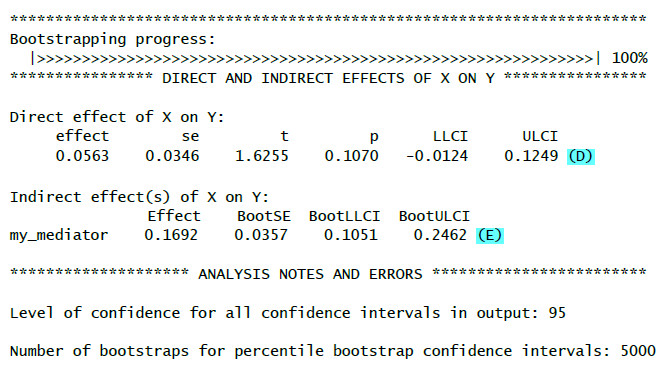
(D): The c'-path for a second time, see (B).
(E): The indirect effect (a*b). It is significant, because the bootstrap confidence interval does not include zero.
BootLLCI and BootULCI: The limits of a CI for b of the indirect effect based on bootstrapping – not on a normality assumption. This is what really counts. To show mediation the indirect effect has to be significant. Significant a-path and b-path are neither necessary nor sufficient for a significant mediation.
6. Additional Parameters
Even though the limited code above gives you the mediation test in many cases you want to have additional information. Following are some additional PROCESS parameters that could be helpful for your mediation model.
Effect size (indirect effect)
If you run a mediation model you can calculate effect sizes (partially standardized = ps, and completely standardized indirect effects = cs) by setting the effsize parameter to 1.
Example:
effsize =1
Total effect
If you run a mediation model you can test the total effect (= c-path) by setting the total parameter to 1.
Example:
total =1
Sobel Test in PROCESS
You can run a Sobel-test by setting the normal parameter to 1.
Example:
normal = 1
(In general I do not recommend using the Sobel test. In small to medium samples it can lead to misleading results and in large samples there are still reasons to prefer the bootstrapping results.)
Standardized Effects
You can get standardized effects for all the regression paths by setting the stand parameter to 1.
Example:
stand =1
Including Covariates
If you want to add covariates to your model you can use cov =... If you have only one covariate you can simply put it into the formula. With more covariates you have to bind them together with c(....).
Examples:
cov = "age"
cov = c("age", "gender")
Number of Bootstrap Samples
By default, for models with bootstrapping the number of bootstrap samples is 5,000. You can change this by setting the boot parameter to the number of samples you would like to have.
Example:
boot = 10000
Bootstrapping Not Only for Indirect Effects
By default, PROCESS uses bootstrapping for the indirect effects. If you want to get robust confidence intervals for the rest of the estimates you can do that by setting the modelbt parameter to 1. Otherwise you would have to test the normality assumption before reporting the test results for the a-path, b-path and c'-path.
Example:
modelbt = 1
Bootstrapping - Start Value for the Random Numbers Generator
Bootstrapping has a random component. Based on a random numbers generator many random samples are drawn from your sample with replacement. As a result, if you repeatedly run an analysis with bootstrapping you will get slightly different results (SE, p-values, confidence intervals) each time you run the analysis. If you want to get the same results each time you can give the random number generator a start value by setting the seed parameter to any integer number. (It is not important which number you choose.) Still you will not get the same results as when running the same model with the same data with PROCESS in SPSS because the random numbers generators of SPSS and R are different.
Example:
seed = 654321
7. My Favorite Mediation R-Code
The following code example for a mediation with two covariates showes the options I tend to use when testing a mediation model:
process (data = my_data_frame, y = "my_DV", x = "my_IV", m ="my_mediator", model = 4, effsize =1, total =1, stand =1, cov = c("my_covariate1", "my_covariate2"), boot = 10000 , modelbt = 1, seed = 654321)
8. Sample Output 2 – Mediation with Additional Options
Here is an example of the output you could get with all those additional options with comments for the additional output elements:
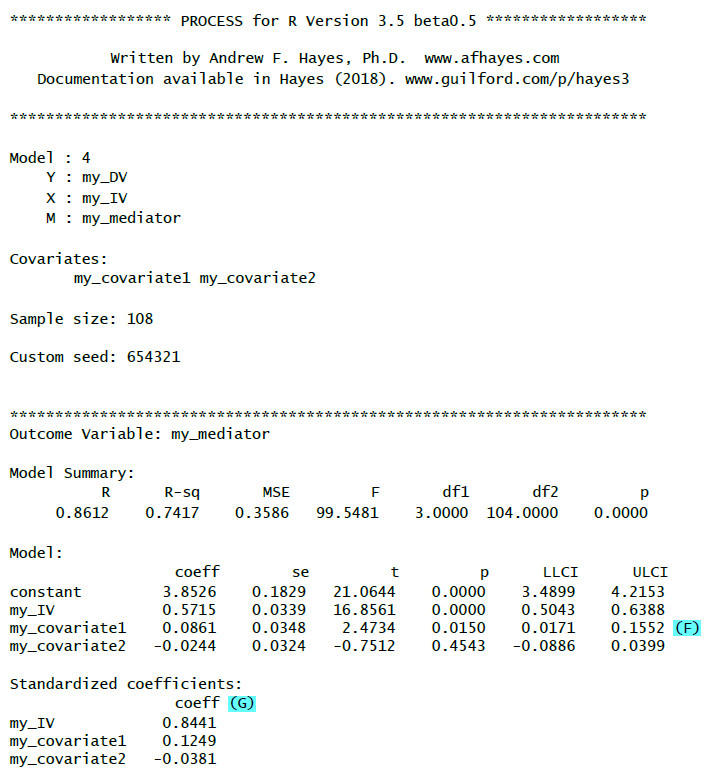
(F): Results for the covariates.
(G): Standardized regression weights (betas)
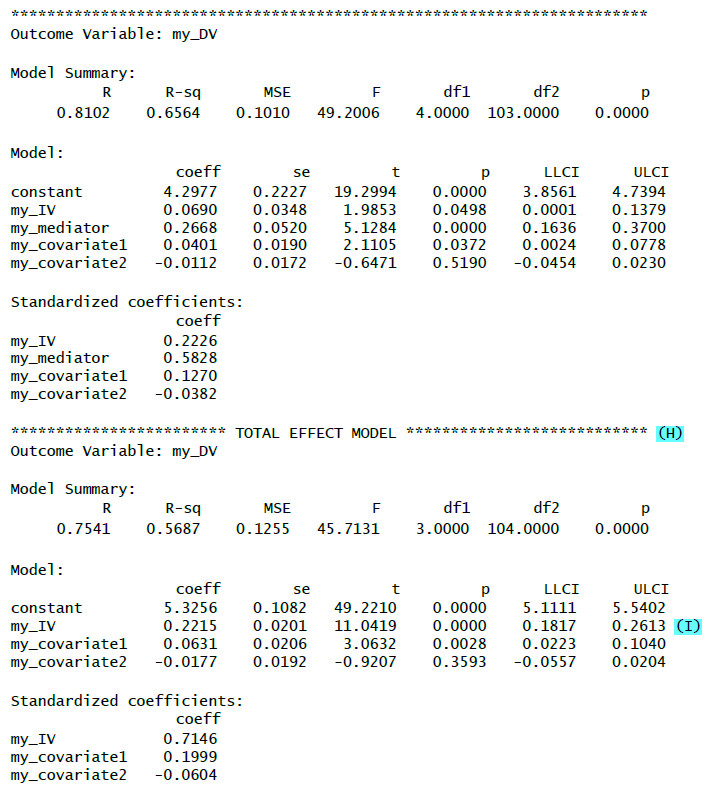
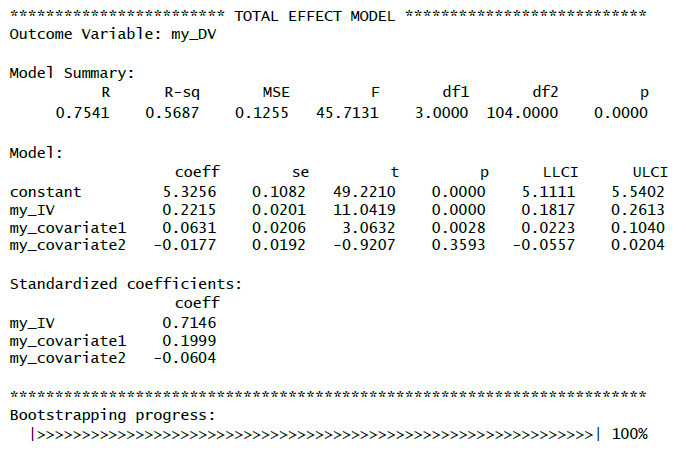
(H): Total effect model = model for the effect of the IV on the DV without looking at a mediator.
(I): Effect of the IV on the DV without looking at a mediator.

(J): ps = Partially standardized effect (standardized dependent variable)
(K): cs = Completely standardized effect (standardized independent and dependent variable)
(L): Partially standardized indirect effect (standardized dependent variable)
(M): Completely standardized indirect effect (standardized independent and dependent variable)
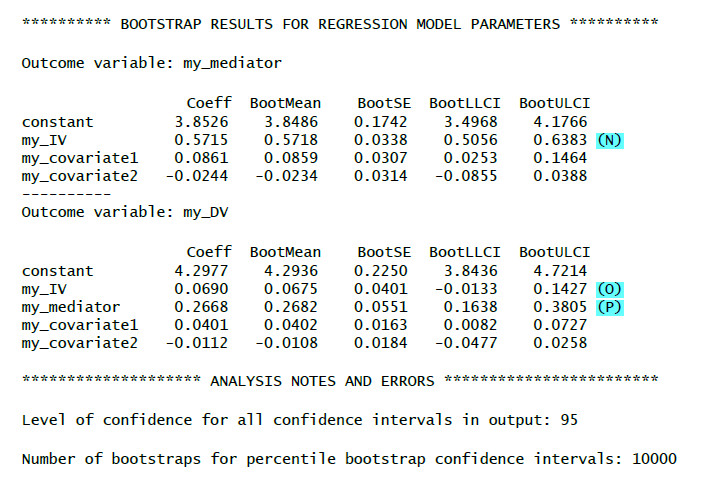
(N): Bootstrap results for the a-path (robust against violations of normality assumption)
(M): Bootstrap results for the c'-path (robust against violations of normality assumption)
(O): Bootstrap results for the b-path (robust against violations of normality assumption)
9. Parallel Mediation
You can use PROCESS model 4 with more than one mediator at once. In that case PROCESS calculates a parallel mediation model where an indirect effect is mediated by more than one mediator parallel to each other (for a serial mediation instead you could use PROCESS model 6).
If you want to use PROCESS model 4 to test a parallel mediation, you have to bind the Mediators with c(......).
Example:
m = c("anger","hostility")
That leads to an additional helpful parameter:
Comparing Indirect Effects in Parallel Mediation
If you run a model with parallel mediation paths (e.g. model 4) you can compare those paths by setting the contrast parameter. If you set it to 1 you get a test for the difference between their regression weights, if you set it to 2 you get a test for the difference of the absolute values of their regression weights. This second value can be useful if you want to compare one positive indirect effect with a negative one in order to assess whether the positive one is (in absolute terms) significantly larger than the negative one.
Examples:
contrast =1
10. Parallel Mediation R-Code
The following code example for a parallel mediation with two mediators (and two covariates) showes the options I tend to use when testing a parallel mediation model:
process(data = my_data_frame, y = "my_DV", x = "my_IV", m =c("my_mediator1", "my_mediator2"), model = 4, effsize =1, total =1, stand =1, cov = c("my_covariate1", "my_covariate2"), contrast =1, boot = 10000 , modelbt = 1, seed = 654321)
11. Sample Output 3 – Parallel Mediation
Here is an example of the output you could get for a parallel mediation with two mediators:
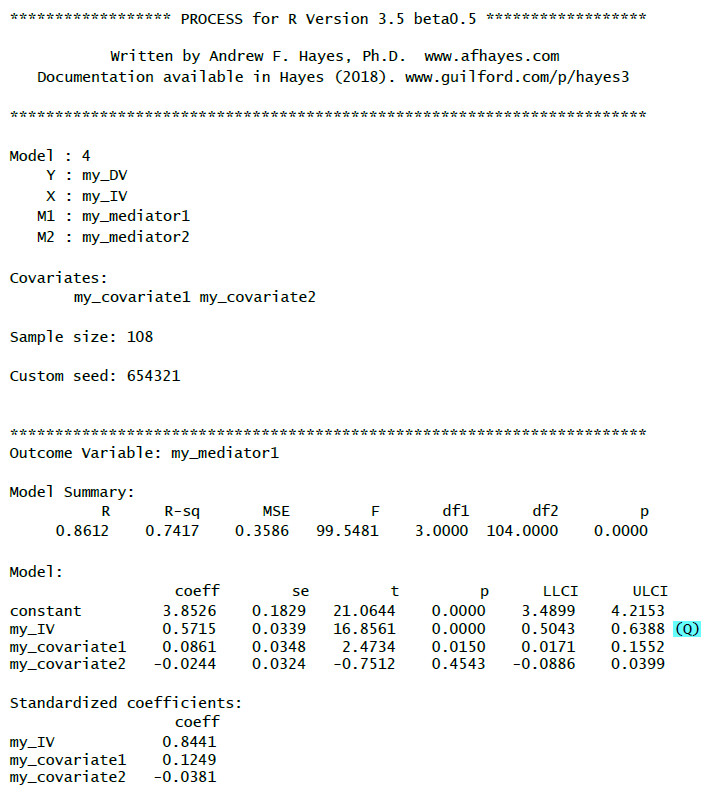
(Q): A-path to the first mediator

(R ): A-path to the second mediator
(S): B-path from the first mediator
(T): B-path from the second mediator

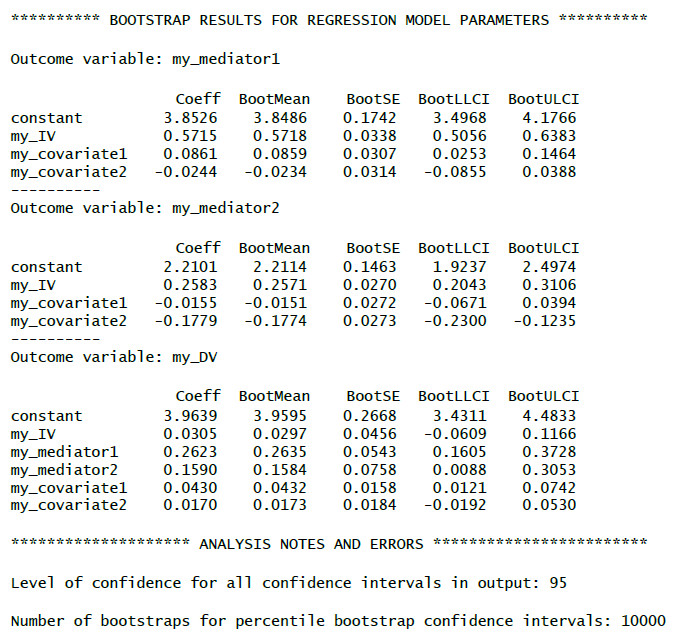
(U): Total indirect effect. Indirect effects mediated by mediator 1 or 2 taken together.
Bootstrapped, here it is significant since the CI does not contain zero.
(V): Indirect effect mediated by mediator 1.
Bootstrapped, here it is significant since the CI does not contain zero.
(W): Indirect effect mediated by mediator 2.
Bootstrapped, here it is significant since the CI does not contain zero.
(X): Contrast between indirect effect mediated by mediator 1 and indirect effect mediated by mediator 2.
Bootstrapped, here it is significant since the CI does not contain zero. So we know that the two indirect effects are significantly different, in this case the indirect effect mediated by the first mediator is significantly stronger than the other indirect effect.
(Y): Contrast definition (important if there are more than two mediators and therefore more than one contrast).
12. More Information
If you want to know more about the theory behind a mediation analysis I recommend Andrew Hayes' excellent book:
“Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach”
http://www.afhayes.com/introduction-to-mediation-moderation-and-conditional-process-analysis.html