What Modification Indices Do Not Tell You
by Arndt Regorz, MSc.
April 7, 2024
Modification indices are an important tool in order to find misspecifications, especially in a confirmatory factor analysis (CFA) or in the measurement model of a structural equation model (SEM).
In general, there are three different model improvements that can be suggest by a modification index:
- Additional factor loadings (cross-loadings)
- Additional covariances (factor covariances and error covariances)
- Additional regression paths in a structural model
But there are at least four possible misspecifications that are not easily detected by modification indices. You have to know these cases to be able to detect possible model misspecifications in your model.
Four Model Misspecifications Not Easily Detected by Modification Indices
1. Item Assigned to the Wrong Factor
Modification indices can suggest additional loadings (cross-loadings). But they can’t tell you that an item should completely change the factor it is assigned to, see as an example figure 1.
Figure 1
Item Assigned to Wrong Factor
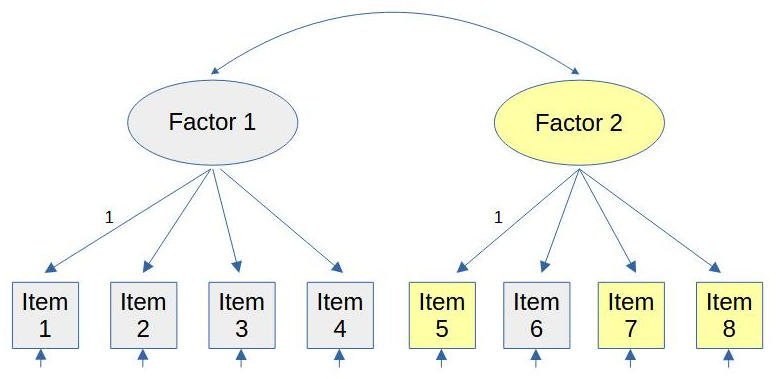
Note. Items with equal colors represent the same true factor.
Here item 6 is assigned to the wrong factor (factor 2 instead of the correct factor 1).
Such a misspecification can be only inferred indirectly. In most cases there will be a modification index suggesting a cross-loading on the correct factor. If after allowing a suggested cross-loading the loading on the original factor is nearly zero and not significant, then you could remove the original loading.
2. Too Many Factors
Another possible misspecification, that the modification indices don’t tell you about, is having too many factors. See as an example figure 2.
Figure 2
Too Many Factors
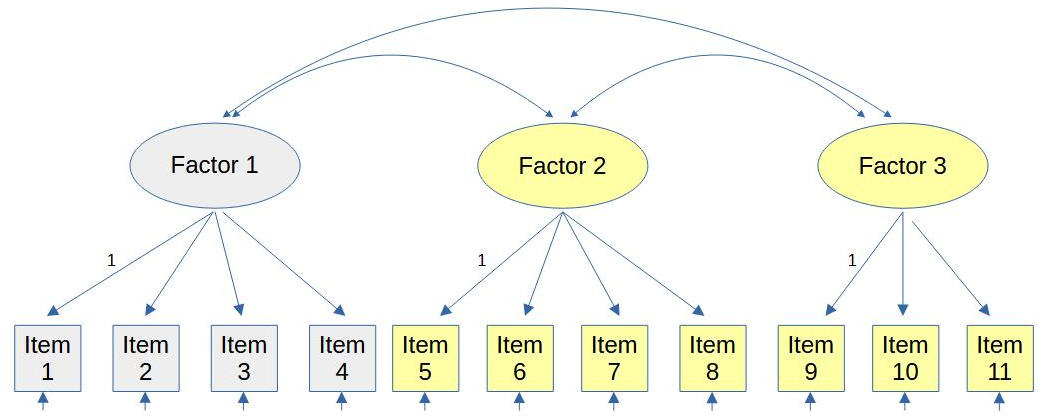
Note. Items with equal colors represent the same true factor.
Here factor 2 and factor 3 are basically one factor. But you won’t get a modification index telling you to merge those two factors.
In order to see this misspecification you have to look at the resulting factor covariance. If, for instance, the standardized covariance (=correlation) between factor 2 and factor 3 was .90, you could conclude that their items belong to a common factor, merge the factors and test the resulting model
3. Not Enough Factors
If you don’t have enough factors in your model then there won’t be a modification index telling you to add an additional factor. As an example see figure 3.
Figure 3
Not Enough Factors
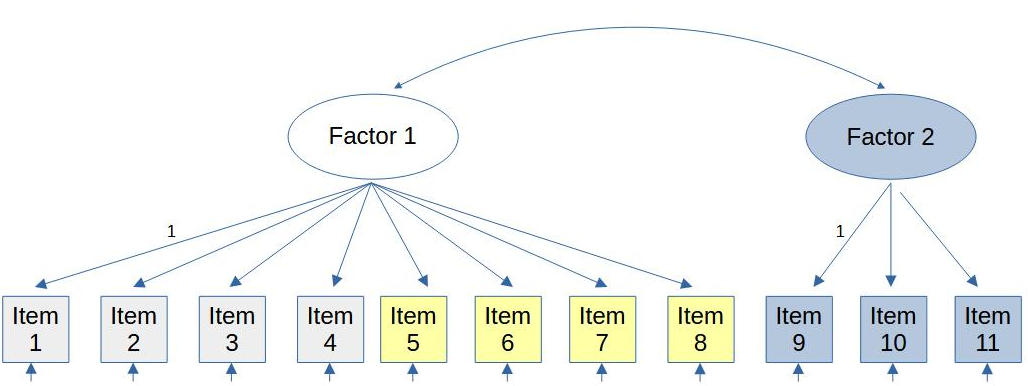
Note. Items with equal colors represent the same true factor.
Here the items assigned to factor 1 actually belong to two separate factors. Even though there won’t be an explicit modification suggestion as part of the modification indices there will be indirect clues.
In a case like this you could see the need for splitting a factor by looking at the suggested error covariances. In the example there could be modification indices for additional covariances between:
item 1 - item 2 - item 3 - item 4, and
item 5 - item 6 - item 7 - item 8
If you see such a structure in the suggested error covariances, i.e. clusters of items with additional covariances within the clusters, that is highly indicative of the need to split the factor.
4. Complex Wrong Factor Structure
If the hypothesized factor structure is completely wrong then it is difficult to see that in modification indices. See as an example figure 4.
Figure 4
Complex Wrong Factor Structure
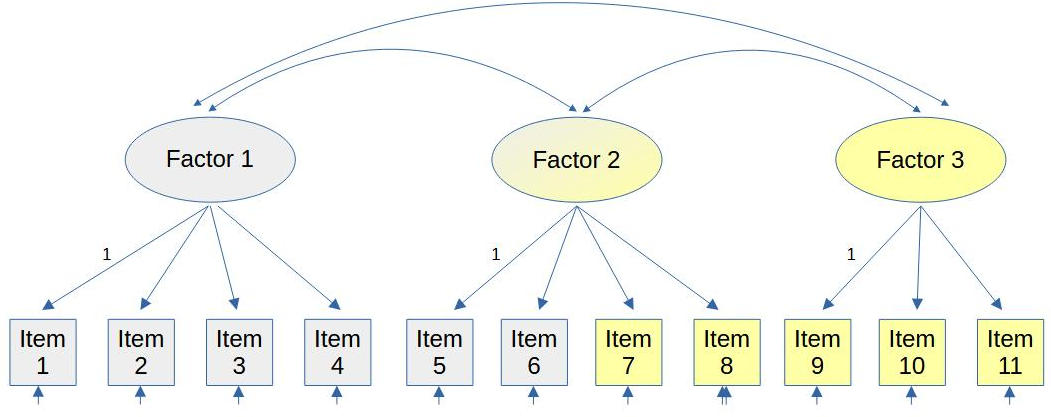
Note. Items with equal colors represent the same true factor.
Here we have hypothesized a three factor structure. The true structure has only two factors but it can’t be reached by simply merging two of the factors into one.
This type of misspecification is probably the most difficult to spot.
I think it is possible that it would show up in the list of modification indices with error covariances (items 5 and 6 correlating with the items 1-4, items 7 and 8 correlating with the items 9-11) and/or with cross-loadings (items 5 and 6 with cross loadings on factor 1, items 7 and 8 with cross loadings on factor 3). But I haven’t come across this situation in my research yet.
Conclusion
Not all possible model misspecifications can be seen directly in the modification indices. Sometimes there is a little bit detective’s work required to deduce the true cause for misspecification from modification indices and item correlations.
Bonus tip
If you have all kinds of modification indices and can’t really make sense of them, then it might help to run an exploratory factor analysis (EFA) in order to see what kind of model changes to start with.
Citation
Regorz, A. (2024, April 7). SEM/CFA: What modification indices do not tell you. Regorz Statistik. http://www.regorz-statistik.de/blog/mod_indices.html