Empirical Underidentification in SEM and CFA

by Arndt Regorz, MSc.
March 24, 2024

One important step in a structural equation model (SEM) or a confirmatory factor analysis (CFA) is model identification. There must be enough independent pieces of information to get to an unique estimate for all model parameters.

This is mostly a theoretical question, answered in advance of acquiring data. But you can also encounter underidentification after the fact, due to an unexpected structure of your empirical data.

Empirical underidentification in a CFA or in the measurement model of an SEM occurs when the model being tested lacks sufficient empirical information from the observed variables to estimate all the parameters accurately even though in theory it should contain enough information. This means that the data does not provide enough information to uniquely determine the values of all the parameters in the specified model.

Several different causes could contribute to empirical underidentification in a measurement model. This blog post shows you three different reasons for that.

Four Reasons for Empirical Underidentification

1. (Non)Correlated Factors with Few Indicators

You probably know that an isolated measurement model with three items is in general just-identified, with two items underidentified. But a measurement model with two correlated factors is overidentified with only two items for each factor.

Figure 1

Measurement Model with Two Correlated Factors

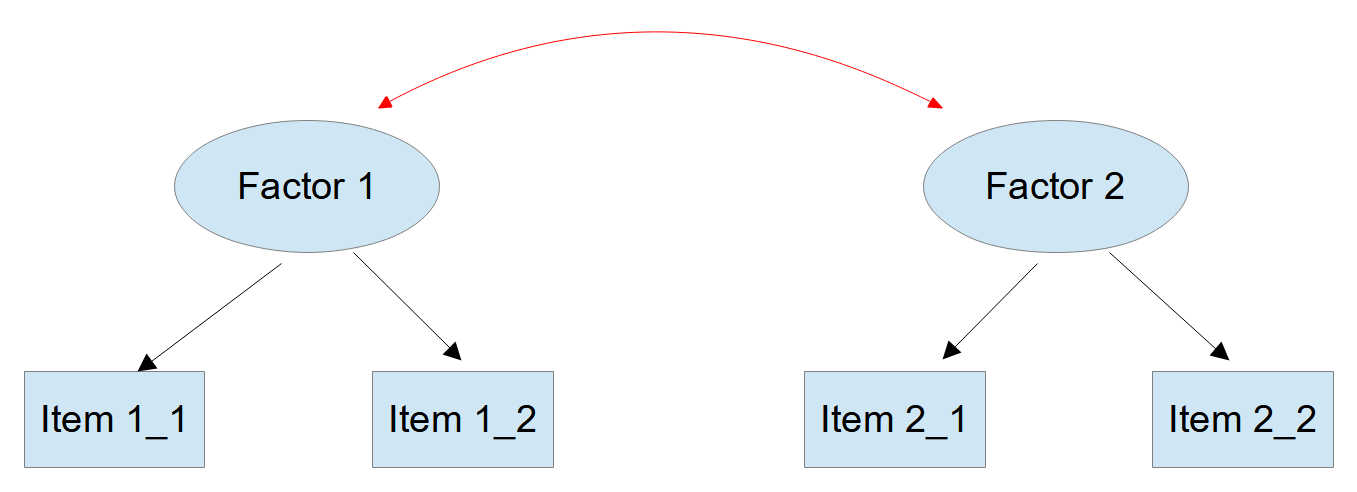
There is a crucial assumption here. The two factors must be truly correlated. If empirically this assumption does not hold then we will have two isolated factors with only two items each. And those are not identified!

You can spot this problem in your data by looking at the intercorrelations between your items. If the items loading on factor 1 show no correlations with the items loading on factor 2, then this could be the cause of your estimation problems.

Such a misspecification can be only inferred indirectly. In most cases there will be a modification index suggesting a cross-loading on the correct factor. If after allowing a suggested cross-loading the loading on the original factor is nearly zero and not significant, then you could remove the original loading.

2. Multicollinearity Between Items

For an isolated factor, in general, three items are enough for a just identified measurement model.

Figure 2

Measurement Model with Three Items

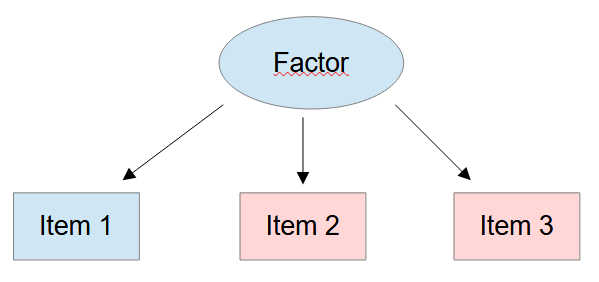
Nevertheless, you could run into problems with a measurement model like this if there is collinearity between at least two of the items. Collinearity (often multicollinearity when more than 2 variables are affected by this) refers to a situation where two or more predictor variables in a model are highly correlated, making it challenging to separate their individual effects on the response variable.

In a situation with collinearity it looks in the model graph as if there were three items for the factor. But, empirically, there are only two independent sources of information to estimate the factor, and that is not enough.

You can spot this problem in your data by looking at the item correlations. If the correlations between items of one factor with, e.g., three items are extremely high then collinearity could be the reason for estimation problems due to empirical underidentification.

3. Unrelated Item

An isolated measurement model is just identified if there are at least three indicator variables (and no error covariances between those). But this presupposes that all three items are connected to the factor.

Figure 3

Three Items

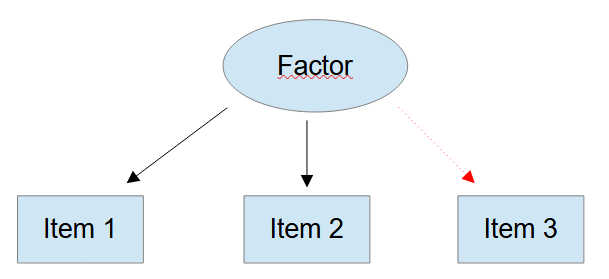
If one of the items does not have a relationship to the other two (i.e., if there is an item in the model that should not be there) then we have only two pieces of empirical information to estimate the model. And that is not enough.

4. Bad Marker Variable

In order to assign a metric to a factor we often use the marker variable approach: The loading of the first item for each factor is constrained to 1.

This can lead to empirical underidentification if this first item does not correlate with the other items of the scale. Because in this case the factor, representing the shared variance of the items, cannot get a metric from an item that has (almost) no relationship with it.

Figure 4

Bad Marker Variable

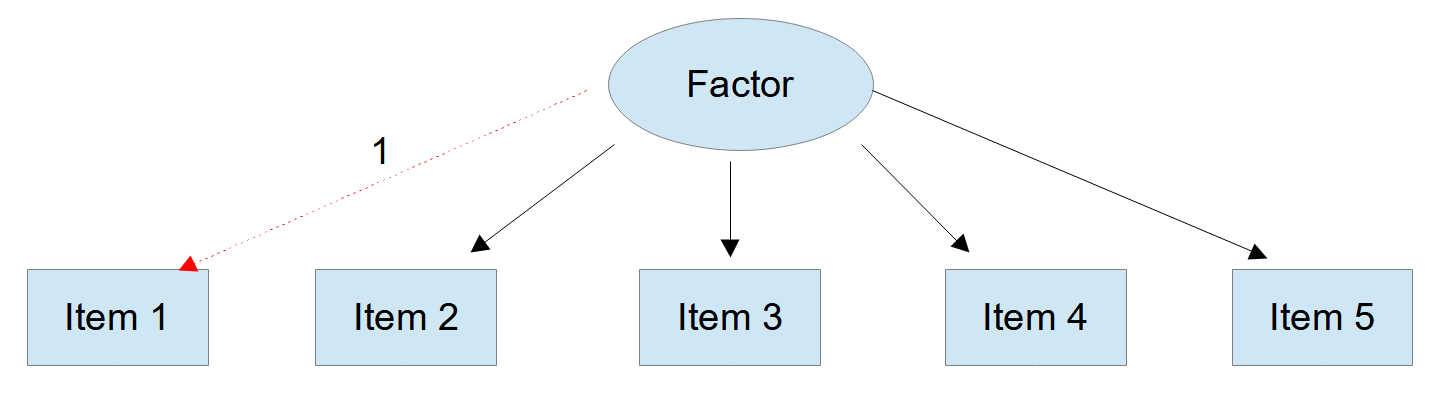
In contrast to the other two possible reasons this can be rectified if there are enough indicators (see problem 3): We just have to change the identification method. We can either constrain the loading of a different item to 1 or instead we can constrain the factor variance to 1. In both cases we will see that the loading for the problematic item will be nearly 0.

Conclusion

Empirical underidentification is a dangerous problem because it only shows its head when it is in many cases too late: after you have run your empirical study.

Therefore, when using new measurements with unknown psychometric properties it is not a good idea to be too frugal with the number of indicator variables for the factors. In those cases, using at least four indicators for each factor could provide an important margin of error against empirical underidentification.

References

Brown, T. A. (2015). Confirmatory factor analysis for applied research. Guilford publications.

Johnson, B., & Hallquist, M. (2017). Full SEM specification [Lecture notes]. Penn State University. https://psu-psychology.github.io/psy-597-SEM/07_full_sem/full_sem_specification.html

Citation

Regorz, A. (2024, March 24). Empirical underidentification in SEM and CFA. Regorz Statistik. http://www.regorz-statistik.de/blog/empirical_underidentification.html