Polynomiale Regression bei verletzter Linearitätsannahme

Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, Stand: 05.09.2022

Eine zu prüfende Regressionsvoraussetzung ist die eines linearen Zusammenhangs (siehe mein Tutorial Linearitätsannahme). Doch was können Sie tun, wenn diese Prüfung zum Ergebnis kommt, dass kein linearer Zusammenhang vorliegt?

Hier ist häufig die polynomiale Regression die praktisch einfachste Alternative zur gewöhnlichen multiplen Regression. Dabei wird neben einem Prädiktor auch noch dessen Quadrat (und ggf. noch höhere Exponenten) mit aufgenommen. Also z.B. als Regressionsgleichung:
AV = b0 + b1 UV + b2 UV² + e

Damit kann man auch nicht-lineare Zusammenhängen modellieren. Wie man das genau macht (auch mit SPSS) und wie die Ergebnisse zu interpretieren sind, wird im folgenden erläutert.

Inhalt

1. Video-Tutorials
2. Problemstellung
3. Grundlagen polynomiale Regression
4. Umsetzung mit der multiplen Regression
5. Interpretation der Ergebnisse
6. Kontrollvariablen oder weitere Prädiktoren
7. Hypothesentests
8. Hypothesentests wenn nicht beide Prädiktoren signifikant sind
9. Polynome höhere Ordnung
10. Aufruf Polynomiale Regression mit SPSS
11. Effektstärke
12. Multikollinearität
13. Polynomiale Regression zur Prognose
14. Quellen

1. YouTube-Video-Tutorials

Polynomiale Regression allgemein:

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

Polynomiale Regression mit R:

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

2. Problemstellung: Zusammenhangshypothese prüfen bei verletzter Linearitätsannahme

Sie haben eine übliche Zusammenhangshypothese aufgestellt nach dem Muster:
Die unabhängige Variable UV steht in einem positiven Zusammenhang mit der abhängigen Variable AV.

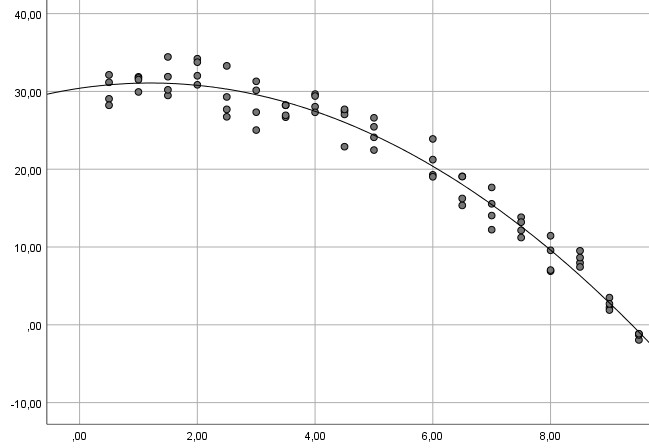
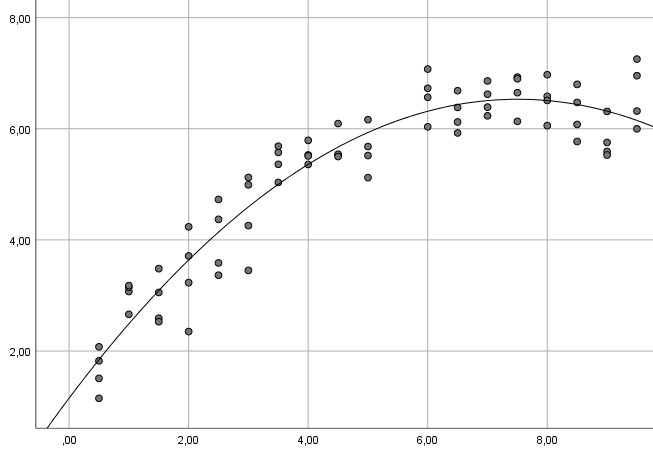
Doch das Streudiagramm zwischen UV und AV, das Sie zur Prüfung der Linearität des Zusammenhangs angefordert hatten, gibt deutliche Hinweise auf einen nicht-linearen Zusammenhang:

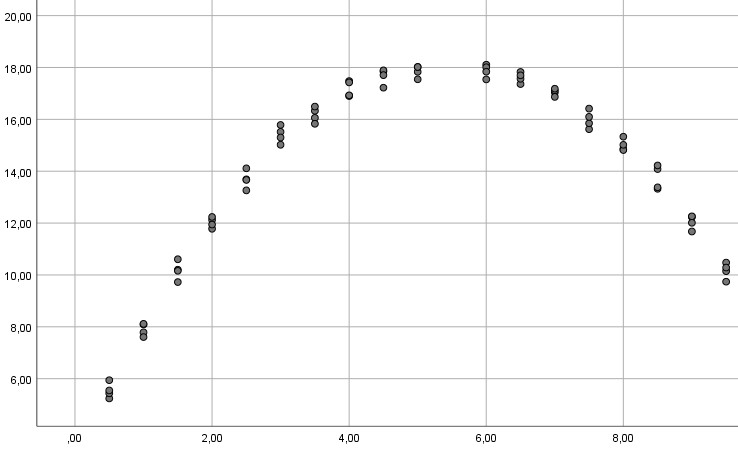
Beispiel 1:

Beispiel 2:

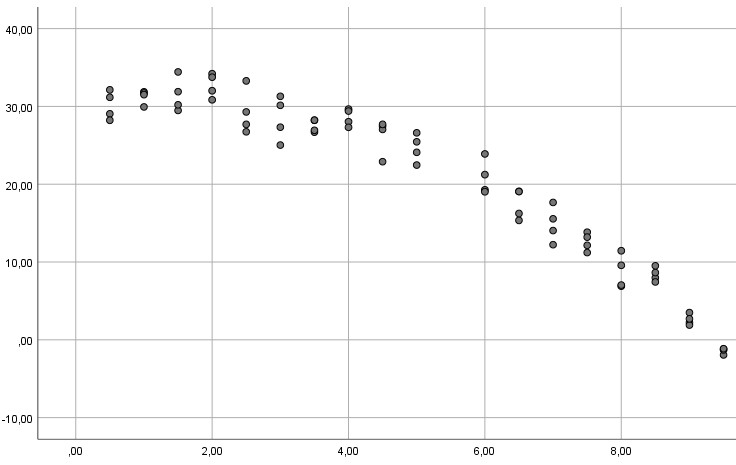
Beispiel 3:

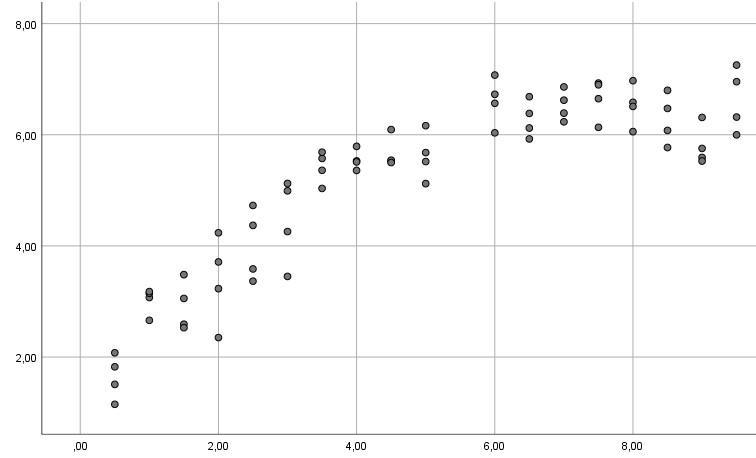
In allen drei Beispielen ist die Linearitätsannahme verletzt (im ersten Beispiel offensichtlich, bei den anderen beiden, wenn man genauer hinguckt), so dass eine gewöhnliche multiple Regression nicht das angemessene Verfahren ist und zu falschen Ergebnissen für Ihren Hypothesentest führen kann (ausführlicher zu diesem Problem siehe mein Tutorial zum Thema Linearitätsannahme). Stattdessen kann man ein polynomiales Modell schätzen.

3. Grundlagen polynomiale Regression

Bei der polynomiale Regression wird keine Gerade an die Daten angepasst, sondern eine komplexere Kurve. Im einfachsten Fall, auf den wir uns hier überwiegend beschränken werden, wird eine Parabel angepasst. Damit kann man gut u-förmige oder umgekehrt u-förmige Zusammenhänge modellieren.

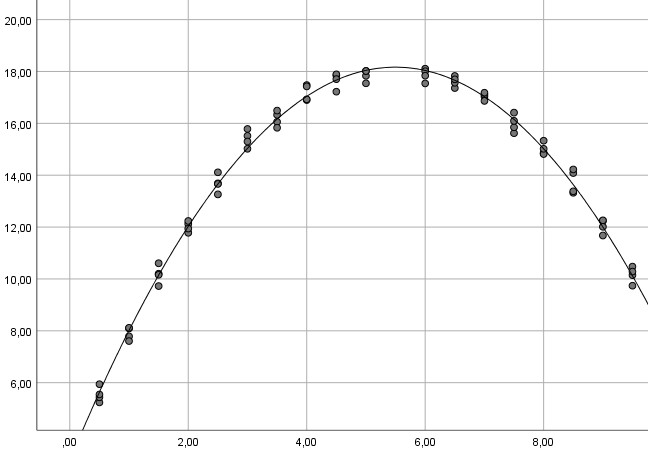
Für die drei o.g. Beispiele würden sich folgende Vorhersagen ergeben:

Beispielkurve 1:

Beispielkurve 2:

Beispielkurve 3:

Die Formel einer Parabel weist neben der unabhängigen Variable x auch noch deren Quadrat mit auf:
AV = b0 + b1 UV + b2 UV² + e

Generell ist eine polynomiale Regression eine Regression, bei der ein Prädiktor mehrfach mit verschiedenen Exponenten in der Modellgleichung auftaucht, im einfachsten Fall eines Polynoms zweiten Grades eine Parabel mit den Exponenten 1 (UV) und 2 (UV²).

4. Umsetzung mit der multiplen Regression

In der Praxis ist die polynomiale Regression recht einfach umzusetzen, da es technisch einfach mit den bekannten Verfahren der multiplen Regression berechnet werden kann. Für denjenigen Prädiktor, für den Sie einen quadratischen Zusammenhang vermuten, nehmen Sie einfach zusätzlich noch dessen Quadrat mit als weiteren Prädiktor in die Regression mit auf. Dass man so etwas machen kann, kennen Sie vielleicht von der Moderationsprüfung – auch dort wird neben einzelnen Prädiktoren zusätzlich ein Produkt (UV * MOD) mit aufgenommen.

Bei der polynomialen Regression ist das genauso, nur ist es hier ein Produkt eines Prädiktors mit sich selbst, also UV * UV, als weiterer Prädiktor. Für das Statistikprogramm ist das kein Problem, denn für das Programm ist auch das Produkt einfach nur eine Zahl – das Programm „sieht“ den Unterschied nicht zu einem normalen einfachen Prädiktor.

Auch die Prüfung der sonstigen Regressionsvoraussetzungen (z.B. Normalverteilung und Homoskedastizität der Residuen) läuft genauso ab, wie Sie es von der multiplen Regression kennen.

5. Interpretation der Ergebnisse

Bei der Interpretation der Ergebnisse gibt es eine Besonderheit im Vergleich zur gewöhnlichen multiplen Regression. Bei der multiplen Regression gibt ein Regressionsgewicht die Veränderung des Kriteriums wieder, wenn sich der Prädiktor um eine Einheit ändert und alle anderen Prädiktoren konstant gehalten werden – also unter „Kontrolle“ der anderen Prädiktoren.

Als Ergebnis der polynomialen Regression erhält man jetzt sowohl ein Regressionsgewicht für die UV als auch ein zweites Regressionsgewicht für dessen Quadrat UV². Aber hier funktioniert die o.g. Interpretationsweise nicht. Denn es kann sich nicht UV ändern, ohne dass sich auch UV² ändert und umgekehrt. Damit macht eine Interpretation eines dieser beiden Regressionsgewichte alleine ohne dessen Gegenstück überhaupt keinen inhaltlichen Sinn.

Der Ausweg aus diesem Problem ist, beide Gewichte (für UV und für UV²) zusammen zu interpretieren. Das macht aus inhaltlich mehr Sinn, da beide Gewichte zusammen einen quadratischen (=parabelförmigen) Zusammenhang abbilden. Insofern ist es primär relevant, ob beide Prädiktoren zusammen signifikant Varianz im Kriterium erklären.

6. Kontrollvariablen oder weitere Prädiktoren

Häufig wollen Sie mehrere Prädiktoren zusammen untersuchen. Sei es, weil Sie mehrere theoretisch bedeutsame Prädiktoren in Ihrem Modell haben, sei es, weil Sie Kontrollvariablen mit einbeziehen wollen.

In diesem Fall bietet sich eine hierarchische Regression an, in der die verschiedenen Prädiktoren blockweise in das zu testende Modell einbezogen werden. Dabei sollte man alle Komponenten eines Polynoms in einem Block einschließen – im Regelfall also UV und UV². Auf diese Weise kann man nämlich auch testen, ob diese unabhängige Variable auf nicht-lineare Weise signifikant Varianz der abhängigen Variable erklärt. Dazu betrachtet man dann nicht primär die Signifikanz der Regressionsgewichte für UV und UV², sondern die Signifikanz des ganzen Regressionsschrittes – ob also delta-R² für diesen Block aus UV und UV² signifikant ausfällt.

In der Regel würde ich diesen nicht-linearen Zusammenhang als letzten Block in das Modell einschließen. Für die anderen Prädiktoren und Kontrollvariablen ist dann primär entscheidend, ob deren Regressionsgewicht signifikant ist. Für den nicht-linearen Zusammenhang kommt es m.E. in erster Linie darauf an, ob der letzte Regressionsschritt mit den Komponenten des Polynoms als Ganzes signifikant mehr erklärt.

7. Hypothesentests

Wie oben sei der Ausgangspunkt eine Hypothese, dass die unabhängige Variable in einem positiven Zusammenhang mit der abhängigen Variable steht – ohne Aussage, dass dieser Zusammenhang linear sein müsse.

Wenn man jetzt ein signifikantes Modell mit einem Polynom zweite Ordnung erhält, also einer Parabel, ist damit die Hypothese bestätigt oder nicht?

An einem konkreten Beispiel: Es wurden mit der Regression für die folgende Modellgleichung
y = b0 + b1 x + b2 x² + e
diese Modellparameter geschätzt, wobei das Modell insgesamt signifikant war:
b0 = 2.5
b1 = 3.2
b2 = 0.4
Der Wertebereich für X betrug [1; 7].

Aus dem signifikanten quadratischen Zusammenhang allein kann man noch nicht schließen, dass die Hypothese bestätigt wurde. Denn nur aus der Existenz eines quadratischen Zusammenhangs folgt noch nicht das Wissen, ob der Zusammenhang im Wertebereich der unabhängigen Variable ansteigt, fällt oder beides.

Nur wenn der quadratische Zusammenhang im Wertebereich ausschließlich steigt, wäre unsere Hypothese eines positiven Zusammenhangs mit den Daten bestätigt. Also werden wir rechnerisch bestimmen, ob wir uns im Wertebereich der unabhängigen Variable im ansteigenden oder fallenden Teil der Parabel befinden, oder in beiden.

Aus der Parameterschätzung ergebe sich folgende Gleichung für den quadratischen Zusammenhang zwischen X und Y:
f(x) = 2.5 + 3.2 x + 0.4 x²
Um festzustellen, ob im o.g. Wertebereich die Kurve ansteigt, fällt oder beides, bestimmen wir zunächst den Extremwert der Kurve. Sie erinnern sich vielleicht noch aus dem Mathematikunterricht in der Schule aus der Analysis I an das relativ abstrakte Thema „Kurvendiskussion“ - hier hat man tatsächlich ein sehr praxisrelevantes Einsatzgebiet dafür.

Um den Extremwert der Kurve zu bestimmen, müssen wir zunächst deren erste Ableitung berechnen. Im Falle einer quadratischen Kurve ist das recht einfach, Betrachten wir es zunächst als Formel, dann am Zahlenbeispiel:
f(x) = b0 + b1 x + b2 x²
f'(x) = b1 + 2 b2 x
Die erste Ableitung wird jetzt gleich Null gesetzt, um den Extremwert zu bestimmen:
0 = b1 + 2 b2 x
x0 = - b1/2b2

Angewendet auf unser o.g. Zahlenbeispiel:
f(x) = 2.5 + 3.2 x + 0.4 x²
f'(x)= 3.2 + 0.8 x
0 = 3.2 + 0.8 x
x0 = - 4

Da der Extremwert außerhalb des Wertebereichs [1; 7] liegt, wissen wir, dass die quadratische Kurve im gesamten Wertebereich steigend oder im gesamten Wertebereich fallend ist. Und wenn man einen beliebigen x-Wert aus dem Wertebereich in die zweite Ableitung einsetzt, erhält man hier im Beispiel einen positiven Wert, also eine positive Steigung, z.B.:
f'(1) = 3.2 + 0.8 = 4

Damit ist die geschätzte quadratische Kurve im gesamten Wertebereich von X ansteigend. Also konnte die Hypothese eines positiven Zusammenhangs zwischen X und Y hier mit der polynomialen Regression bestätigt werden.

8. Hypothesentest, wenn nicht beide Prädiktoren signifikant sind

Hinsichtlich der Signifikanz der beiden einzelnen Prädiktoren (UV und UV²) gibt es als Ergebnis der polynomialen Regression vier Möglichkeiten:

• Vorweg: Beide werden signifikant. Das weitere Vorgehen in diesem Fall wurde im vorherigen Abschnitt dargestellt.
• Beide sind nicht signifikant. Dann konnte die Zusammenhanghypothese nicht bestätigt werden.
• Nur der einfache Prädiktor wird signifikant, nicht der quadratische. Das deutet auf einen linearen Zusammenhang hin.
• Nur der quadratische Prädiktor wird signifikant, nicht der einfache. In diesem Fall sollte man m.E. dennoch im Modell den einfachen Prädiktor eingeschlossen lassen, da sich ein quadratischer Zusammenhang im Sinne einer Parabel aus einem quadratischen und einem linearen Teil zusammensetzt. Wenn beide Prädiktoren zusammen signifikant sind, kann man das aus meiner Sicht so interpretieren, dass man einen signifikanten parabelförmigen Zusammenhang vorliegen hat. Dessen weitere Prüfung ist im vorherigen Abschnitt beschrieben.

9. Polynome höhere Ordnung

Bisher wurde der Fall eines Polynoms zweiter Ordnung behandelt, also einer Parabel. Diese kann man z.B. zur Modellierung eines u-förmigen oder umgekehrt u-förmigen Zusammenhangs nutzen. Theoretisch könnte der Zusammenhang jedoch auch als ein Polynom höherer Ordnung modelliert werden, also z.B. zusätzlich mit einem Term für x³.

Damit könnte man theoretisch sogar solche Zusammenhänge modellieren:

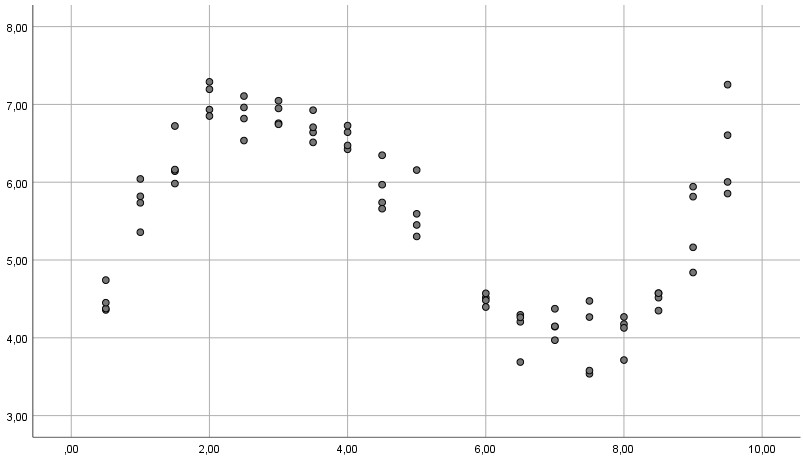
Allerdings ist das für gewöhnliche Zusammenhangshypothesen mit einigen Problemen verbunden:

• Je komplexer das an die Daten angepasste Modell, desto größer ist das Risiko, dass das Ergebnis mehr Besonderheiten der vorliegenden Stichprobe widerspiegelt und nicht den tatsächlichen Zusammenhang in der Grundgesamtheit.
• Gleichzeitig wird auch die Hypothesenprüfung aufwändiger, weil man bei einem signifikanten Zusammenhang eine Kurvendiskussion der resultierenden Modellgleichung durchführen muss, um analytisch den Verlauf der Kurve im Wertebereich der unabhängigen Variable festzustellen.
• Theoretisch sind derartige Zusammenhänge schwer begründbar. Ein u-förmiger oder umgekehrt u-förmiger Zusammenhang ist in bestimmten Situationen alles andere als abwegig. Aber für einen Verlauf wie die o.g. Kurve fallen mir zumindest spontan keine relevanten Praxisfälle beispielsweise aus der Psychologie ein, für die ich theoretisch so einen Zusammenhang erwarten würde.

Insofern ist rein technisch ein Polynom höherer Ordnung einfach zu prüfen, indem man Terme für x³ usw. zusätzlich zu x und x² einschließt. Aber für die Prüfung einer Zusammenhangshypothese erscheint mir das in der Regel nicht wirklich sinnvoll zu sein.

10. Aufruf Polynomiale Regression mit SPSS

Sie haben eine unabhängige Variable UV und eine abhängige Variable AV und wollen einen quadratischen Zusammenhang untersuchen. Dann können Sie das aus SPSS so aufrufen:

Aus dem Menü:

Zunächst legen Sie einen Term für den quadratischen Effekt an:

Transformieren->Variable Berechnen
„Zielvariable“ eingeben, z.B. UV2
„Numerischer Ausdruck:“ UV * UV
„OK“

Dann führen Sie eine ganz gewöhnliche multiple Regression mit UV und UV2 durch:

Analysieren->Regression->Linear
AV in das Feld „Abhängige Variable“
UV und UV2 in das Feld „Unabhängige Variable(n)“

Entweder „OK“ klicken oder vorher noch die Prüfungen der Voraussetzungen auswählen:

Auf „Statistiken klicken“
dort Haken setzen für „Kollinearitätsdiagnose“, und „Fallweise Diagnose“ (mit Einstellung „3 Standardabweichungen“)
ggf. noch Haken bei „Durbin-Watson“
Dann auf „Weiter“ klicken

Auf „Diagramme“ klicken
Haken für „Histogramm“ und „Normalverteilungsdiagramm“ setzen
in das Y-Feld von „Streudiagramm“ *SRESID ziehen
in das X-Feld von „Streudiagramm“ *ZPRED ziehen
Auf „Weiter“ klicken

Auf „OK“ klicken zum Ausführen der Auswertung

Aufruf polynomiale Regression mit SPSS-Syntax

*Anlegen des quadratischen Terms.

COMPUTE UV2 = UV * UV.
EXECUTE.

*Durchführung der Regression mit Voraussetzungsprüfung hinsichtlich Normalverteilung, Homoskedastizität, Multikollinearität, Ausreißern.

REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT AV
/METHOD=ENTER UV UV2
/SCATTERPLOT=(*SRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID) NORMPROB(ZRESID)
/CASEWISE PLOT(ZRESID) OUTLIERS(3).

Der gleiche Aufruf zusätzlich mit zwei Kontrollvariablen KVA und KVB:

*Anlegen des quadratischen Terms.

COMPUTE UV2 = UV * UV.
EXECUTE.

*Durchführung der Regression mit Voraussetzungsprüfung hinsichtlich Normalverteilung, Homoskedastizität, Multikollinearität, Ausreißern.

REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL CHANGE
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT AV
/METHOD=ENTER KVA KVB
/METHOD=ENTER UV UV2
/SCATTERPLOT=(*SRESID ,*ZPRED)
/RESIDUALS HISTOGRAM(ZRESID) NORMPROB(ZRESID)
/CASEWISE PLOT(ZRESID) OUTLIERS(3).

11. Effektstärke

Als Effektstärke für die polynomiale Regression bietet sich das quadrierte Bestimmtheitsmaß R² an, das die durch die Regression erklärte Varianz im Kriterium anzeigt. Und bei einem hierarchischen Vorgehen, das bei der Existenz von Kontrollvariablen oder anderen zusätzlichen Prädiktoren sinnvoll wäre, würde man das delta-R² für den Einschluss einer Variable (also z.B. für einen Block mit dem Einschluss von x und x² als zusätzliche Prädiktoren) betrachten.

12. Multikollinearität

Ein Problem, das bei der polynomialen Regression typischerweise auftritt, ist das der Multikollinearität, also der linearen Abhängigkeit zwischen verschiedenen Prädiktoren. Wenn jetzt sowohl die UV als auch UV * UV als Prädiktoren in die Regression einbezogen sind, führt dies häufig zu einer starken Multikollinearität. Damit einher gehen häufig hohe Standardfehler und damit sehr breite Konfidenzintervalle bzw. nicht signifikante Hypothesentests für einzelne Regressionsgewichte.

Eine denkbare Gegenmaßnahme gegen Multikollineariät besteht im Zentrieren der unabhängigen Variable und anschließendem Einschluss der zentrierten UV und deren Quadrat als Prädiktoren in die Regressionsgleichung.

Damit wird das übliche Maß für Multikollinearität, der Varianzinflationsfaktor (VIF), in der Regel deutlich reduziert. Für den quadratischen Prädiktor UV * UV ändert sich jedoch weder die Schätzung des unstandardisierten Regressionsgewichts b noch dessen Standardfehler (Baltes-Götz, 2019; Dalal & Zickar, 2012) oder dessen Signifikanz. Es ändert sich hingegen in der Regel das Ergebnis für den einfachen Prädiktor UV. Das beruht jedoch darauf, dass jetzt inhaltlich ein etwas anderes Modell getestet wird – es wird jetzt nicht mehr die unabhängige Variable als Prädiktor berücksichtigt, sondern die Abweichung der unabhängigen Variable von ihrem eigenen Mittelwert.

Insofern kann man eine Zentrierung durchführen, wenn man die geänderte Interpretation der Ergebnisse beachtet. Notwendig zur Vermeidung der Multikollinearität ist es in diesem Fall jedoch nicht.

13. Polynomiale Regression zur Prognose

Bisher wurde der Einsatz der polynomialen Regression zum Test einer Zusammenhangshypothese vorgestellt. Es gibt jedoch noch ein zweites Einsatzfeld für Regressionsanalysen: die Prognose von Werten. Welchen Wert hat die abhängige Variable bei einem bestimmten Wert der unabhängigen Variable?

Hier ist beim Einsatz einer polynomialen Regression folgende Einschränkung zu beachten: Wenn ein nicht-linearer Zusammenhang an die Daten angepasst wird, dann gilt diese Anpassung zunächst einmal nur für den Wertebereich der unabhängigen Variable.

Beispiel:
Sie nehmen Alter als unabhängige Variable und schätzen ein polynomiales Modell mit irgendeiner abhängigen Variable. Wenn Sie in Ihren Daten einen Wertebereich für die unabhängige Variable zwischen 20 und 50 hatten, dann können Sie aus Ihrem Modell in der Regel keine sinnvollen Schlüsse für die Ausprägung der abhängigen Variable bei Personen mit einem Alter von 10 Jahren oder von 70 Jahren ziehen.

Diese Einschränkung gilt zwar im Prinzip auch bei der gewöhnlichen linearen Regression, aber im Fall der polynomialen Regression ist dieses Problem häufig stärker ausgeprägt.

14. Quellen

Baltes-Götz, B. (2019). Lineare Regressionsanalyse mit SPSS. [Rev. 190107]. Retrieved from: https://www.uni-trier.de/fileadmin/urt/doku/linreg/linreg.pdf

Dalal, D. K., & Zickar, M. J. (2012). Some common myths about centering predictor variables in moderated multiple regression and polynomial regression. Organizational Research Methods, 15, 339-362. doi:10.1177/1094428111430540

Gujarati, D. (2009). Basic Econometrics (4th edition). New Delhi, India: Tata McGraw-Hill.

Stimson, J. A., Carmines, E. G., & Zeller, R. A. (1978). Interpreting polynomial regression. Sociological Methods & Research, 6, 515-524. doi:10.1177/004912417800600405

Wie kann ich Sie weiter unterstützen?

Beratung für Datenauswertung bei Bachelorarbeit oder Masterarbeit

Welche Auswertungen sind für Ihre Fragestellung richtig und was müssen Sie dabei beachten? Schon in einer Stunde (Telefon/Skype/vor Ort) kann man viele Fragen klären. Auf meiner Seite zu Statistik-Beratung finden Sie weitere Informationen.