Moderatoranalyse - Teil 1:
Grundlagen der moderierten Regression

Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, Stand: 19.11.2024

Eine der häufigsten sozialwissenschaftlichen Fragestellung ist die nach einer möglichen Moderation: Wie wird der Zusammenhang zwischen einer unabhängigen und einer abhängigen Variable davon beeinflusst, welchen Wert eine drittes Variable, der Moderator, einnimmt?

Das folgende Tutorial zeigt die Grundlagen der moderierten Regression sowie deren Umsetzung mit SPSS.

Inhalt

1. Video-Tutorial
2. Was ist Moderation?
3. Abgrenzung zur Mediation
4. Beispiele
5. Modell in der moderierten Regression
6. Interaktion vs. Moderation
7. Moderatoranalyse interpretieren
8. Zentrierung
9. Power (Teststärke) bei Moderation
10. Follow-Up-Analysen
11. Moderatoranalyse SPSS Syntax
12. Interpretation der SPSS-Auswertung
13. Ausblick: Moderatoranalyse mit PROCESS-Makro (Version 3)
14. Moderation Ergebnisse berichten
15. Quellen

1. YouTube-Video-Tutorial

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

2. Was ist Moderation?

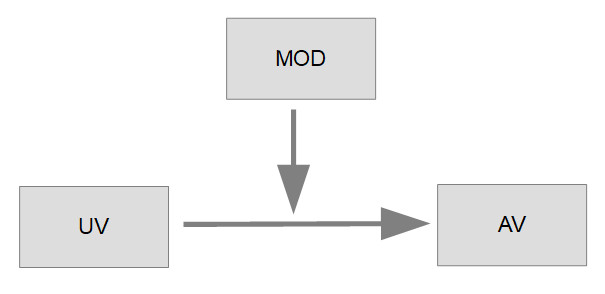
Bei Moderation geht es im Grundmodell um die Frage, ob der Zusammenhang zwischen einer unabhängigen Variable UV und einer abhängigen Variable AV von einer dritten Variable, dem Moderator, beeinflusst wird.

Als praktisches Beispiel kann man sich einen Moderationseffekt wie die Gangschaltung eines Autos (oder eines Fahrrads) vorstellen:

Die Umdrehung des Motors ist dabei die unabhängige Variable. Die Umdrehung der Räder und Reifen ist die abhängige Variable. Und der eingeschaltete Gang ist der Moderator: Vom Gang hängt der Zusammenhang zwischen der Motordrehung und der Drehung der Räder ab. Die gleiche Motordrehung führt je nach eingelegtem Gang zu unterschiedlichen Drehungen der Räder.

Ein Moderator kann dabei sowohl dichotom als auch kontinuierlich sein. Einer der häufigsten dichotomen Moderatoren ist das Geschlecht: Der Zusammenhang zwischen einer unabhängigen und einer abhängigen Variable unterscheidet sich je nach Geschlecht der untersuchten Person. Als kontinuierlicher Moderator kommt beispielsweise die Ausprägung auf einer Skala zu einer Persönlichkeitseigenschaft in Frage.

3. Abgrenzung zur Mediation

Ähnlich wie bei der Mediation geht es auch bei der Moderation im einfachsten Fall um den Zusammenhang von drei Variablen. Jedoch ist dieser Zusammenhang sowohl theoretisch als auch von der statistischen Prüfung her ein anderer.

Bei der Mediation wird ein indirekter Effekt untersucht – der Mediator ist dabei die Variable, die den Effekt der unabhängigen Variable auf die abhängige Variable vermittelt (mehr dazu in meinen Mediations-Tutorials). Bei der Moderation hingegen geht es nicht darum, auf welchem Weg ein Effekt wirkt. Sondern es geht darum, wovon die Stärke (und ggf. Richtung) eines Effekts abhängt.

Als Merksatz:
Mediation fragt „Auf welchem Weg?“, Moderation fragt „Wovon hängt die Stärke ab?“

4. Beispiele

Es folgen zwei Beispiele für Moderatoreffekte aus der Forschungspraxis. Das erste Beispiel weist einen kontinuierlichen Moderator auf, das zweite einen dichotomen.:

Arbeitsplatzunsicherheit und kontraproduktives Arbeitsverhalten
Der Zusammenhang zwischen Arbeitsplatzunsicherheit und kontraproduktivem Arbeitsverhalten (wie z.B. Diebstahl, Gerüchte verbreiten etc.) wurde moderiert durch die Persönlichkeitseigenschaft Ehrlichkeit/Bescheidenheit: Bei Personen mit geringer Ehrlichkeit/Bescheidenheit war eine größere Arbeitsplatzunsicherheit mit mehr kontraproduktivem Arbeitsverhalten verbunden. Bei Personen mit hoher Ehrlichkeit/Bescheidenheit gab es diesen Zusammenhang nicht (Chirumbolo, 2015).

Ehequalität und Depressivität
Der Zusammenhang zwischen Ehequalität und späterem Anstieg von Depressivität wurde moderiert durch das Geschlecht: Der Zusammenhang war für Frauen stärker als für Männer (Dehle & Weiss, 1998).

5. Modell in der moderierten Regression

Zur Prüfung, ob eine Variable MOD den Zusammenhang zwischen einer unabhängigen Variable UV und einer abhängigen Variable AV moderiert, führt man eine multiple Regression durch. Dabei schließt man ein die unabhängige Variable, den vermuteten Moderator und das Produkt aus unabhängiger Variable und Moderator als Prädiktoren und untersucht deren Einfluss auf die abhängige Variable:

AV = b0 + b1 UV + b2 MOD + b3 UV MOD + e

Eine Moderation liegt dann vor, wenn das Regressionsgewicht für den Produktterm (= für die Interaktion) signifikant wird, also b3. Das gilt aber nur dann, wenn auch UV und MOD wie in dieser Gleichung zusätzlich als einzelne Prädiktoren eingeschlossen sind (man darf also nicht nur die Interaktion einschließen ohne zusätzlichen Einschluss des Moderators).

Häufig führt man eine hierarchische moderierte Regression durch, bei der man in zwei Schritten vorgeht. Im ersten Schritt schließt man nur die einfachen Prädiktoren ein (UV, MOD), also noch ohne Produktterm:

Schritt 1: AV = b0 + b1 UV + b2 MOD + e

Im zweiten Schritt wird dann zusätzlich noch der Produktterm eingeschlossen:

Schritt 2: AV = b0 + b1 UV + b2 MOD + b3 UV MOD + e

Dabei ist neben der Signifikanz von b3 vor allem interessant, wie viel zusätzliche Varianz das Modell mit Produktterm (und damit die Moderation) erklären kann im Vergleich zum Modell ohne Produktterm.

Technisch ist die Prüfung einer Moderation also eine multiple Regression, jedoch mit einer wichtigen Abweichung zu den üblichen Modellen: Neben einzelnen Prädiktoren (UV, MOD) ist auch das Produkt aus zwei Prädiktoren (UV x MOD) enthalten. Das ist jedoch für die Auswertungstechnik kein Problem: Ein Statistikprogramm erkennt nicht den Unterschied zwischen einem einzelnen Prädiktor und dem Produkt aus zwei Prädiktoren – auch das Produkt ist für die Software nur eine Zahl, auf die das Programm die ganz normale Optimierungsrechnung der Kleinst-Quadrate-Regression anwendet.

6. Interaktion vs. Moderation

Bevor wir uns näher mit der Interpretation der Ergebnisse einer moderierten Regression befassen können, müssen wir uns mit der Abgrenzung zwischen „Interaktion“ und „Moderation“ auseinandersetzen.

Im vorherigen Schritt wurde gezeigt, dass man bei einer Moderationshypothese prüft, ob die Interaktion zwischen unabhängiger Variable und Moderator einen signifikanten Einfluss hat. Daraus könnte man schließen, dass Moderation und Interaktion das gleiche sind.

Doch wenn Sie sich die Modellgleichung der moderierten Regression genau ansehen, werden Sie feststellen, dass man außer von den Namen her gar nicht feststellen kann, welcher Prädiktor die unabhängige Variable ist und welcher Prädiktor der Moderator. Eine Interaktion ist bidirektional, es ist statistisch gar kein Unterschied, ob z.B. das Einkommen mit dem Geschlecht interagiert oder das Geschlecht mit dem Einkommen.

Daher muss man zwei Aspekte voneinander unterscheiden: den theoretischen und den statistischen.

Auf der Ebene der Theorie prüft man bei einer Moderation eine kausale Wirkung: Inwieweit wird ein kausaler Effekt einer unabhängigen Variable auf eine abhängige Variable von einer dritten Variable, dem Moderator, beeinflusst? Aus der Theorie ergibt sich daher, was die unabhängige Variable ist und was der Moderator.

Auf der Ebene der statistischen Prüfung hingegen ist keine Richtung vorgegeben. Hier wird zur Prüfung einer Moderationshypothese lediglich der Interaktionseffekt zweier Variablen geprüft.

Das bedeutet, dass inhaltlich verschiedene Hypothesen (B moderiert den Zusammenhang zwischen A und C, A moderiert den Zusammenhang zwischen B und C) statistisch mit demselben Modell geprüft werden (Interaktion von A und B bei der Vorhersage von C).

Bei der Formulierung der Ergebnisse muss man allerdings vorsichtig sein. Sehr häufig werden Moderationshypothesen mit korrelativen Studien (z.B. Fragebogen) geprüft. Korrelative Studien können jedoch keine Kausalität beweisen. Je nachdem, wie genau der Prüfer ist, muss man dann bei der Darstellung im Ergebnisteil (anders als im Theorieteil) darauf achten, dass man Formulierungen wie „unabhängige Variable“, „abhängige Variable“, „bewirkt“ usw. vermeidet und eher von „Prädiktor“, „Kriterium“, „hängt zusammen“ spricht. Hier sind allerdings die Geschmäcker von verschiedenen Prüfern sehr unterschiedlich, es gibt auch welche, die genau das Gegenteil lesen wollen, weil eine kausale Theorie geprüft wird.

7. Moderatoranalyse interpretieren

Wie können Sie jetzt die verschiedenen Regressionsgewichte bei einer moderierten Regression interpretieren?

Die Modellgleichung wurde oben vorgestellt als:
AV = b0 + b1 UV + b2 MOD + b3 UV MOD + e

Diese Modellgleichung kann man umformen, was die Interpretation m.E. sehr erleichtert:
AV = (b0 + b2 MOD) + (b1 + b3 MOD) UV + e

Das kann man sich jetzt wie eine einfache Regression vorstellen, die jedoch vom Moderator abhängt. Der Inhalt der ersten Klammer ist der Achsenabschnitt (Intercept) der Regressionsgerade und der Inhalt der zweiten Klammer ist die Steigung (Slope) der Regressionsgerade.

Wir haben also bei der Moderation nicht eine einzige Regressionsgerade, sondern so viele verschiedene Geraden, wie der Moderator an Ausprägungen hat. Man spricht auch von bedingten Regressionsgeraden (conditional effects) – unter der Bedingung, dass der Moderator eine bestimmte Ausprägung hat.

Die einzelnen Regressionsparameter kann man auf dieser Basis wie folgt interpretieren:

• b0 ist der Achsenabschnitt der Regressionsgerade, wenn der Moderator den Wert von Null annimmt.
• b2 ist der Betrag, um den der Achsenabschnitt der Regressionsgerade sich von b0 unterscheidet, wenn der Moderator um eine Einheit steigt.
• b1 ist die Steigung der Regressionsgerade, wenn der Moderator den Wert von Null annimmt.
• b3 ist der Betrag, um den die Steigung der Regressionsgerade sich von b1 unterscheidet, wenn der Moderator um eine Einheit steigt.

Von einer Moderation spricht man dann, wenn b3 signifikant von Null verschieden ist, wobei dieser Parameter nur interpretierbar ist, wenn beide Einzeleffekte im Modell eingeschlossen sind.

Die bei multiplen Regressionen häufig auch übliche Interpretation von standardisierten Gewichten (betas) ist bei der Moderation eher problematisch. Das hängt damit zusammen, dass das Produkt aus zwei standardisierten Prädiktoren in der Regel etwas anderes ist als ein standardisiertes Produkt. Sie sollten also besser die unstandardisierten Regressionsgewichte interpretieren.

8. Zentrierung

Häufig wird die Moderatorvariable zentriert, bevor man eine moderierte Regression durchführt. Es wird also für jede Beobachtung vom Wert der Moderatorvariable deren Mittelwert für die Stichprobe abgezogen, so dass die zentrierte Variable einen Mittelwert von Null hat. (Wie man das praktisch mit SPSS macht, wird weiter unten in der Beispielsyntax gezeigt). Dafür werden zwei Gründe in der Literatur diskutiert, ein sinnvoller und ein weniger sinnvoller.

Der sinnvolle Grund für eine Zentrierung liegt in der leichteren Interpretation der Regressionsgewichte. Sie hatten im vorherigen Abschnitt gelesen, dass b0 und b1 Achsenabschnitt und Steigung der Regressionsgerade für den Fall sind, dass der Moderator eine Ausprägung von Null annimmt. Wenn man jetzt zentriert, bedeutet eine Ausprägung von Null für die Moderatorvariable, dass man den mittleren Wert des Moderators betrachtet.

Damit präzisiert sich die Interpretation von b0 und b1 bei Zentrierung:

• b0 ist der Achsenabschnitt der Regressionsgerade bei durchschnittlichem Wert des Moderators
• b1 ist die Steigung der Regressionsgerade bei durchschnittlichem Wert des Moderators

Das Zentrieren ist insbesondere dann sinnvoll, wenn sonst der Wert von Null für den Moderator in den Daten gar nicht vorkommt bzw. nicht sinnvoll interpretierbar ist.

Beispiel:
Der Moderator wird auf einer Likert-Skala von 1 bis 7 gemessen. Dann kommt also ein Wert von 0 schon theoretisch gar nicht vor. Damit ist es weder interessant noch sinnvoll, die Steigung der Regressionsgerade bei diesem irrealen Wert zu betrachten.

Eine Ausnahme von der Empfehlung zur Zentrierung liegt dann vor, wenn es sich beim Moderator um eine dichotome Variable handelt. Dort kann man die Effekte in der Regel besser interpretieren, wenn man auf die Zentrierung verzichtet.

In diesem Fall kann man nämlich ohne Zentrierung b0 und b1 wie folgt interpretieren, falls die Moderatorvariable die Werte 0 und 1 annimmt:

• b0 ist der Achsenabschnitt der Regressionsgerade bei der Moderatorausprägung 0 (also z.B. beim Geschlecht mit 0: Männer und 1: Frauen der Achsenabschnitt für die Männer)
• b1 ist die Steigung der Regressionsgerade bei der Moderatorausprägung 0 (also z.B. beim Geschlecht mit 0: Männer und 1: Frauen die Steigung für die Männer)

Wenn die dichotome Moderatorvariable in Ihren Ausgangsdaten jedoch ein anderes Wertepaar annimmt, wie z.B. 1 und 2, dann empfiehlt sich zur besseren Interpretierbarkeit deren Umcodierung auf 0 und 1.

Der weniger sinnvolle Grund für eine Zentrierung hat mit Multikollinearität zu tun. Multikollinearität ist ein potentielles Problem in multiplen Regressionsanalysen. Sie entsteht, wenn mehrere Prädiktoren voneinander linear abhängig sind. Das kann in einer moderierten Regression tatsächlich relativ leicht passieren. In der Literatur wurde teilweise die Ansicht vertreten, dass eine Zentrierung des Moderators hier ein wirksames Gegenmittel wäre. Zwischenzeitlich wurde jedoch gezeigt, dass das ein Irrglaube war und Zentrierung bei der Moderationsanalyse das Multikollinearitätsproblem bei der Regressionsschätzung nicht reduzieren kann.

Zusammenfassend kann man also zur Zentrierung sagen: Sie ist bei nicht-dichotomen Moderatoren häufig sinnvoll, weil sich dann die verschiedenen Effekte besser interpretieren lassen. Bei dichotomen Moderatoren jedoch ist die Interpretation bei unzentriertem Moderator in der Regel einfacher.

Bei der Ergebnisinterpretation ist zu beachten, dass sich durch die Zentrierung das Regressionsgewicht b3 der Interaktion nicht ändert. Die Regressionsgewichte b1 für den Prädiktor und b2 für den Moderator hingegen ändern sich durch die Zentrierung.

Häufig wird neben einem kontinuierlichen Moderator auch noch eine kontinuierliche unabhängige Variable zentriert. Das wiederum erleichtert ggf. die Interpretation des Regresionsgewichts für den Moderator.

9. Power (Teststärke) bei Moderation

Die Teststärke ist in derartigen Untersuchungen leider häufig reduziert. Dafür gibt es zwei Gründe:

Eine verringerte Reliabilität reduziert in der Regel die Möglichkeit, einen Effekt aufzudecken. Und bei dem Produktterm in der Moderationsanalyse reduziert sich dessen Reliabilität als Produkt der Reliabilitäten beider Einzelteile. Wenn also die unabhängige Variable eine interne Konsistenz von .7 hat und die Moderatorvariable ebenfalls eine interne Konsistenz von .7, dann beträgt die Reliabilität des Produktterms lediglich .49.

Das zweite Problem für die Teststärke beruht auf dem Phänomen der Range Restriction. Es lassen sich am besten Effekte finden, wenn die Prädiktoren eine große Schwankungsbreite aufweisen. Wenn hingegen Prädiktoren überwiegend Werte in einem relativ schmalen Bereich aufweisen (Range Restriction), sind signifikante Effekte schwer zu finden.

Range Restriction ist vor allem ein Problem bei Fragebogenstudien, da dort häufig die Antworten und deren Skalenwerte in der Nähe des jeweiligen Mittelwertes liegen. In diesem Fall ist dann auch die Bandbreite des Produktterms reduziert. Damit lassen sich signifikante Interaktionen in Fragebogenstudien häufig nur in sehr großen Stichproben finden (z.B. über 500, siehe Judd, Yzerbyt, & Muller, 2014). Bei echten Experimenten besteht dieses Problem weniger, da durch eine geeignete experimentelle Intervention eher eine größere Bandbreite bei der unabhängigen Variable und beim Moderator erzeugt wird.

Praktisch bedeutet das für die Poweranalyse, z.B. mit G*Power, dass die zu erwartende Stärke des für die Moderation relevanten Interaktionseffekts gut abgewogen werden sollte. Hier einfach zu sagen „Ich gehe von einem mittleren Effekt aus“ wird häufig zu einer Stichprobengröße führen, die das Auffinden von signifikanten Effekten nur im Ausnahmefall ermöglicht. Stattdessen ist es sinnvoll, sich an den Ergebnissen möglichst vergleichbarer veröffentlichter Studien mit Interaktionseffekten zu orientieren, soweit diese die relevanten Effektgrößen für den Interaktionsterm veröffentlicht haben.

10. Follow-Up-Analysen

Wenn man eine signifikante Interaktion gefunden hat, weiß man nur, dass die Daten mit einem Moderatoreffekt konsistent sind. Man weiß aber noch nicht, wie genau dieser Effekt beschaffen ist. Daher setzt man verschiedene Techniken von Follow-Up-Untersuchungen ein.

Wichtig: Voraussetzung für die folgenden Follow-Up-Untersuchungen ist, dass ein Moderatoreffekt nachgewiesen worden ist, dass es also eine signifikante Interaktion gibt. Ohne diese führen die folgenden Follow-Up-Untersuchungen möglicherweise in die Irre.

Nachfolgend werden drei Methoden dargestellt, wie man eine signifikante Moderation weitergehend auswerten kann:

• Simple Slopes graphisch
• Simple Slopes Hypothesentest
• Signifikanzregion nach Johnson&Neyman

Simple Slopes graphisch

Die einfachste Follow-Up-Untersuchung ist, Regressionsgeraden für verschiedene Stufen des Moderators zu betrachten. Es geht also um also bedingte Regressionsgeraden (Regressionsgerade unter der Bedingung, dass der Moderator einen bestimmten Wert hat). Hier sind zwei Fälle zu unterscheiden:

Dichotomer Moderator (z.B. Geschlecht):
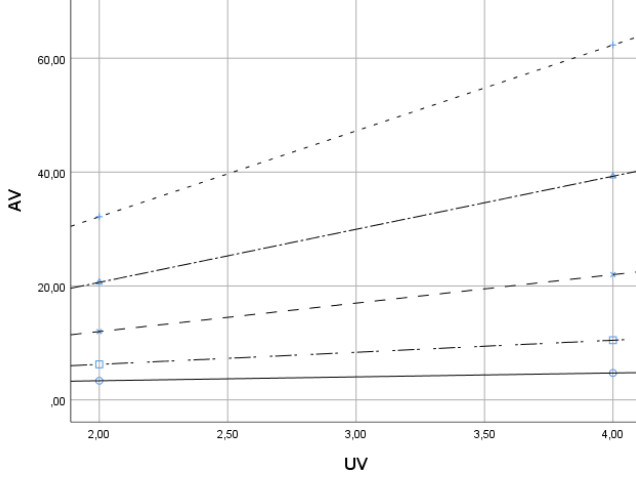
Bei einem dichotomen Moderator gibt es nur zwei mögliche Ausprägungen des Moderators. Daher werden hier zwei Regressionsgeraden betrachtet, nämlich für die beiden Stufen der Moderatorvariable. Im Falle des Geschlechts als Moderator gibt es also je eine Gerade für männliche und für weibliche Versuchtsteilnehmer.

Kontinuierlicher Moderator (z.B. Einkommen):
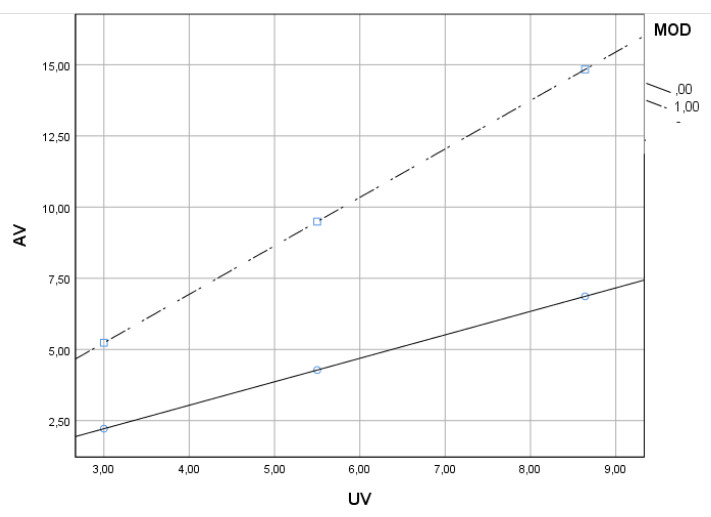
Wenn Sie hingegen einen kontinuierlichen Moderator haben, dann lassen nicht mehr alle möglichen Werte für den Moderator grafisch darstellen. Daher erfolgt eine Auswahl. In der Regel nimmt man zum einen den Mittelwert des Moderators, also die Regressionsgerade für den Fall, dass der Moderator durchschnittlich stark ausgeprägt ist. Und zum anderen nimmt man je einen Moderatorwert unter und über dem Mittelwert – beispielsweise je eine Standardabweichung über bzw. unter der Mitte.

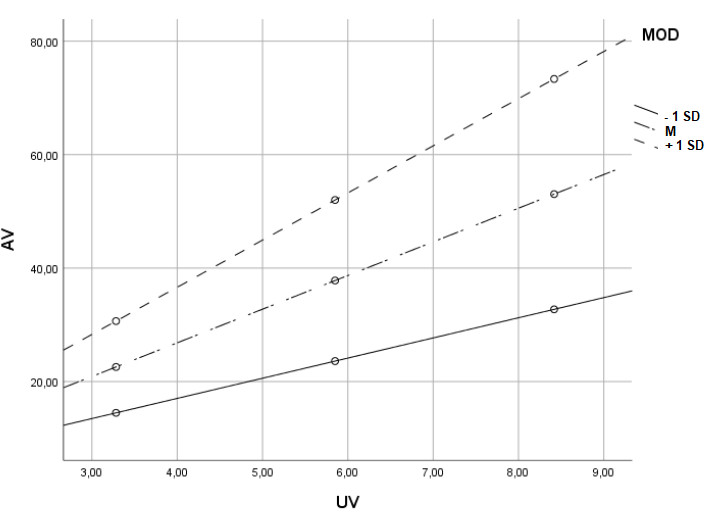
Bei einer sehr schiefen Verteilung kann es jedoch vorkommen, dass ein Moderatorwert von einer Standardabweichung über oder unter dem Mittelwert außerhalb des Wertebereichs des Moderators liegt. Dann ist es besser, zusätzlich zum Mittelwert des Moderators zwei Perzentile zu nehmen – beispielsweise das 16. und das 84. Perzentil.

Simple Slopes Hypothesentest

Zusätzlich zur optischen Betrachtung der Simple Slopes ist es auch sinnvoll, für diese jeweils einen Signifikanztest durchzuführen. Für jeder der oben dargestellten Stufen wird also geprüft, ob die (bedingte) Steigung der Regressionsgerade signifikant von Null verschieden ist.

Im Falle eines dichotomen Moderators sind das also zwei Hypothesentests (für die Ausprägungen 0 und 1 des Moderators), bei einem kontinuierlichen Moderator sind es i.d.R. drei Tests (für den Mittelwert des Moderators sowie je einen Wert über und unter dem Mittelwert).

Wie oben erwähnt, sind diese Tests nur dann aussagekräftig, wenn der Interaktionsterm in der Hauptanalyse signifikant geworden ist. Bei nicht signifikanter Interaktion sind die Tests für Simple Slopes nicht zuverlässig zu interpretieren.

Beispiel: Sie haben einen dichotomen Moderator. Die Simple Slope für die eine Ausprägung des Moderators ist signifikant, für die andere hingegen nicht. Dann dürfen Sie daraus nicht auf eine signifikante Interaktion schließen, wenn nicht auch in der eigentlichen Moderationsprüfung das Regressionsgewicht für den Produktterm signifikant geworden ist.

Signifikanzregion nach Johnson&Neyman

Bei einem kontinuierlichem Moderator haben die oben vorgestellten Simple Slopes einen wichtigen Nachteil: die Auswahl der Werte für den Moderator, für den diese berechnet und getestet werden, ist relativ willkürlich.

Bei dem Verfahren der Signifikanzregion nach Johnson und Neyman wird ermittelt, für welche Werte im Rahmen des Wertebereichs des Moderators (also für welche Region) die bedingten Regressionsgeraden signifikant sind. Dabei können verschiedene Ergebnisse herauskommen:

• Für alle Moderatorwerte im Wertebereich sind die bedingten Regressionsgeraden signifikant.
• Für keinen Moderatorwert im Wertebereich sind die bedingten Regressionsgeraden signifikant.
• Es gibt einen Punkt, an dem die Signifikanz wechselt. Über diesem Moderatorwert sind die Regressionsgerade signifikant/nicht signifikant, unter diesem Moderatorwert sind sie nicht signifikant/signifikant.
• Es gibt zwei Punkte, an denen die Signifikanz wechselt.

11. Moderatoranalyse SPSS

Im Folgenden werden von mir als Variablennamen uv, mod und av verwendet, dafür sollten Sie Ihre eigenen Variablennamen einsetzen.

SPSS-Syntax zur moderierten Regression

Mit der nachstehenden Syntax können Sie eine vermutete Moderation auf Signifikanz testen.

Um eine moderierte Regression direkt mit SPSS durchzuführen, müssen Sie zunächst eine neue Variable für die Interaktion anlegen, anschließend folgt die eigentliche Regression.

*Erzeugen einer Interaktionsvariable.

COMPUTE inter =uv * mod.
EXECUTE.

*Hierarchisch moderierte Regression mit Diagnose der Regressionsvoraussetzungen.

REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS R ANOVA COLLIN TOL CHANGE
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT av
/METHOD=ENTER uv mod
/METHOD=ENTER inter
/PARTIALPLOT ALL
/SCATTERPLOT=(*SDRESID ,*ZPRED)
/RESIDUALS DURBIN HISTOGRAM(ZRESID) NORMPROB(ZRESID)
/CASEWISE PLOT(ZRESID) OUTLIERS(3).

Bei Problemen mit den Regressionsvoraussetzungen kann es sinnvoll sein, diese Auswertung mit Bootstrapping durchzuführen.

Mit Zentrierung

Zur besseren Interpretation kann es sinnvoll sein, den Moderator vorher zu zentrieren, soweit es sich nicht um einen dichotomen Moderator handelt.

*Zentrierung des Moderators.

AGGREGATE
/OUTFILE=* MODE=ADDVARIABLES
/BREAK=
/mod_mean=MEAN(mod).

COMPUTE mod_zentr=mod - mod_mean.
EXECUTE.

In diesem Fall müssten Sie alle o.g. Auswertungen (inkl. dem Erzeugen der Interaktionsvariable) mit der Variable mod_zentr statt der Variable mod durchführen.

Aufruf über das Menü

Vorweg: Der Aufruf einer Moderation über das Menü ist aus meiner Sicht nicht zu empfehlen, dazu gibt es zu viele Einzelschritte. Wenn Sie nur kurz eine Moderation über das Menü testen wollen, dann würde ich eher empfehlen, das über das PROCESS-Makro zu tun. Dennoch sollen im Folgenden die nötigen Schritte gezeigt werden, z.B. auch dafür, wenn Sie selbst Ihre Syntax erstellen wollen (dann im Folgenden statt auf "OK" jeweils auf "Einfügen" klicken.

Zunächst legen Sie (ggf. nach Zentrierung des Moderators) die Interaktionsvariable an:

• Transformieren->Variable_berechnen
• in das Feld "Zielvariable" z.B. "Interaktion" eintragen
• als numerischen Ausdruck: uv * mod
• "OK"

Anschließend rufen Sie die Regression auf: (im Folgenden ohne die zusätzlichen Teilschritte zur Prüfung der Regressionsvoraussetzungen erläutert)

• Analysieren->Regression->linear
• av ins Feld "Abhängige Variable"
• uv und mod ins Feld "Unabhängige Variable(n)"
• auf "Nächste" (oberhalb des Feldes für unabhängige Variablen) klicken
• Interaktion ins Feld "Unabhängige Variable(n)
• auf Schaltfläche "Statistiken" klicken
• Haken bei "Änderung in R-Quadrat" setzen und auf "Weiter" klicken"
• "OK"

12. Interpretation der SPSS-Auswertung

Das Ergebnis der eigentlichen Moderation ist auf dieser Art und Weise leicht festgestellt. Auf die übliche und notwendige(!) Prüfung der Regressionsvoraussetzungen gehe ich im Folgenden nicht gesondert ein; diese unterscheidet sich nicht grundsätzlich von der gewöhnlichen multiplen Regression.

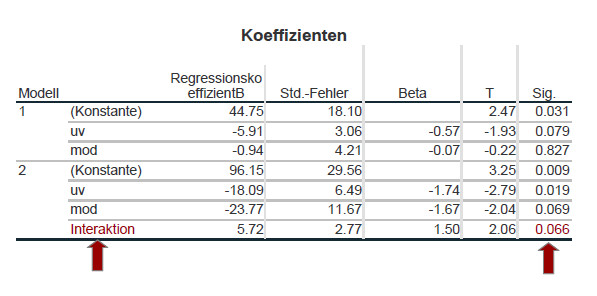
Entscheidend für die Moderationshypothese ist Schritt/Modell 2 des hierarchischen Regressionsmodells in der Tabelle „Koeffizienten“. Hier kommt es darauf an, ob das Regressionsgewicht des zusätzlich zur unabhängigen Variable uv und zum Moderator mod im zweiten Schritt aufgenommen Interaktionsterms inter signifikant von Null verschieden ist (also dort in der Spalte Sig. ein Wert < .05). Wenn ja, dann moderiert die Moderatorvariable mod den Zusammenhang zwischen der unabhängigen Variable uv und der abhängigen Variable av, wenn nein, dann liegt keine Moderation vor.

Hier das Ergebnis einer moderierten Regression, bei der sich die vermutete Moderation nicht als signifikant herausstellte (für den Interaktionsterm p=.066, also größer als .05):

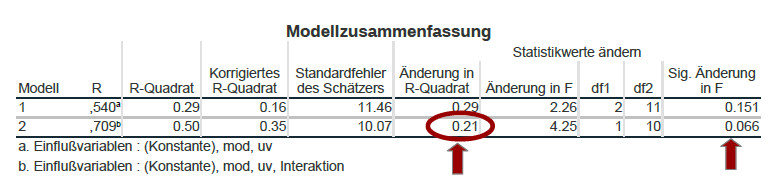
Wenn Sie als Effektstärke wissen wollen, welchen Anteil der Varianz in der abhängigen Variable av die Interaktion aus unabhängiger Variable und Moderator zusätzlich erklärt, betrachten Sie in der Tabelle „Modellzusammenfassung“ die Spalte „Änderung in R-Quadrat“ und dort die Zeile für Modell 2.

Hier im Beispiel ergibt sich eine (aufgrund der sehr kleinen Stichprobe nicht signifikante) Erhöhung der erklärten Varianz durch Einschluss des Interaktionsterms von delta-R²=.21, also 21% der Varianz.

Wenn Sie keinen signifikanten Interaktionseffekt finden, dann ist hier die Analyse im Grunde schon zu Ende. Wenn Sie jedoch eine signifikante Interaktion gefunden haben, steht im nächsten Schritt eine Follow-Up Untersuchung an, wie genau diese Interaktion/Moderation wirkt. Das ist per Hand in SPSS allerdings sehr aufwändig und umständlich, was uns zum PROCESS-Makro führt.

13. Ausblick: Moderatoranalyse mit PROCESS-Makro (Version 3)

Im Gegensatz zur Mediation kann man die eigentliche Moderationsanalyse auch ganz gut direkt mit SPSS ohne das PROCESS-Makro durchführen. Wenn man jedoch eine signifikante Moderation findet, dann zeigt PROCESS seine Stärken: Man kann dort sehr einfach die in diesem Tutorial gezeigten Follow-Up-Analysen gleich mit aufrufen.

Näheres dazu finden Sie in meinem Tutorial „Moderation mit PROCESS Version 3“.

14. Moderation Ergebnisse berichten

Wie stellt man jetzt die Ergebnisse einer moderierten Regression dar?

Hier bietet sich wie für Regressionen üblich eine Tabelle an. In der sechsten Auflage des APA-Manuals (American Psychological Association, 2010) gibt es eine Beispieltabelle für eine moderierte Regression (Table 5.13 auf S. 145), an der man sich orientieren kann. Allerdings ist dort ein umfangreicheres Modell mit insgesamt vier Schritten dargestellt worden. Außerdem wurden dort in einer Tabelle gleich drei abhängige Variablen untersucht, es werden da also drei Regressionen und nicht nur eine abgebildet, so dass für andere sinnvolle Informationen (Teststatistiken, genaue p-Werte) kein Platz mehr war.

Eine denkbare sehr ausführliche Tabellendarstellung einer hierachisch moderierten Regression mit zwei Schritten wäre (wobei Sie dort AV; UV und MOD durch Ihre inhaltlichen Konstrukte/Variablennamen ersetzen müssten):

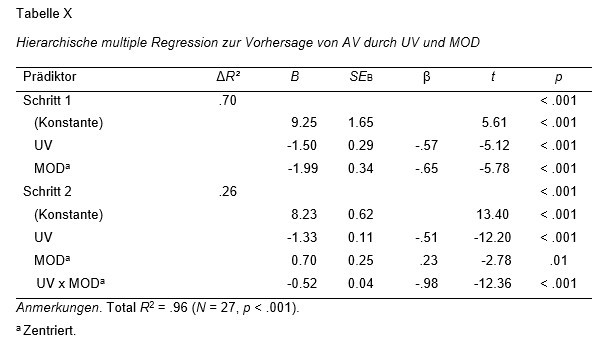
Achtung: Diese Tabelle beruht auf einem anderen Datensatz als die Outputtabellen vom o.g. Punkt 12 (Interpretation der SPSS-Auswertung).

15. Quellen

American Psychological Association. (2010). Publication manual of the American Psychological Association (6th ed). Washington DC: Author.

Baltes-Götz, B. (2018). Mediator- und Moderatoranalyse mit SPSS und PROCESS [Rev. 181007]. Retrieved from: https://www.uni-trier.de/fileadmin/urt/doku/medmodreg/medmodreg.pdf

Chirumbolo, A. (2015). The impact of job insecurity on counterproductive work behaviors: The moderating role of honesty–humility personality trait. The Journal of psychology, 149, 554-569. doi:10.1080/00223980.2014.916250

Dehle, C., & Weiss, R. (1998). Sex differences in prospective associations between marital quality and depressed mood. Journal of Marriage and Family, 60, 1002-1011. doi:10.2307/353641

Field, A. (2013). Discovering statistics using IBM SPSS statistics: And sex and drugs and rock 'n' roll (4th edition). Los Angeles, CA: SAGE.

Hayes, A. F. (2018). Introduction to mediation, moderation, and conditional process analysis: A regression-based perspective (2nd ed.). New York, NY: The Guilford Press.

Judd, C. M., Yzerbyt, V. Y., & Muller, D. (2014). Mediation and moderation. In H. T. Reiss & C. M. Judd (Eds.), Handbook of research methods in social and personality psychology (2nd ed.), (pp. 653-676). Cambridge, UK: Cambridge University Press.

SPSS Tutorials (o.D.). How to Mean Center Predictors in SPSS? Retrieved from: https://www.spss-tutorials.com/spss-mean-center-predictors-for-regression-with-moderation-interaction/

Weitere Tutorials zur Moderationsanalyse:

• Moderationsanalyse mit dem PROCESS-Makro für SPSS
  Moderatoranalyse 2
• Moderation mit dem PROCESS-Makro für R
  Moderatoranalyse mit PROCESS (für R)
• Moderationsanalyse mit JASP
  JASP Video-Tutorial Moderation
• Power/Stichprobenplanung für Moderationsanalysen
  Moderatoranalyse G*Power