Bootstrapping bei Regression
Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, Stand: 06.12.2024
Sie werten Daten mit multipler Regression aus und suchen ein Verfahren, das robust gegen eine Verletzung der Normalverteilungsannahme ist?
Dann ist Bootstrapping ein nonparametrisches Verfahren, das Ihnen weiterhelfen kann.
Inhalt
- Video-Tutorial
- Zusatzmaterialien zum Video
- Anwendungsbereich bei Multipler Regression
- Wie funktioniert Bootstrapping?
- Beispiel
- BCa-Konfidenzintervalle
- Größe der Stichprobe
- Aufruf in SPSS
- Interpretation der SPSS Auswertung
- Testergebnisse berichten
- Quellen
1. YouTube-Video-Tutorial
(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)
2. Zusatzmaterialien zum Video
SPSS-Aufruf BCa-Bootstrapping bei Regressionen (pdf)
Beispiele und Übungsaufgaben Interpretation SPSS Auswertung Bootstrapping bei Regression (pdf)
3. Anwendungsbereich
Bootstrapping als sogenanntes robustes Verfahren kann für sehr unterschiedliche Auswertungen eingesetzt werden (z.B. auch beim t-Test). Hier wird der Einsatz bei der linearen multiplen Regression beschrieben.
Warum sollte man Bootstrapping anwenden?
Die lineare Regression setzt bestimmte Verteilungseigenschaften voraus (Normalverteilung der Residuen), die bei Bootstrapping als nonparametrischem Verfahren nicht nötig sind. Weiterhin wird Varianzhomogenität (Homoskedastitzität) vorausgesetzt, gegen deren Verletzung Bootstrapping auch relativ robust ist.
Denn wenn die angenommenen Verteilungseigenschaften verletzt werden, hat das (ohne Bootstrapping) Konsequenzen: Die geschätzten Parameter bei der multiplen Regression sind zwar weiterhin korrekt. Aber die Standardfehler der Parameter werden falsch geschätzt (in der Regel zu niedrig). Auch bei Heteroskedastizität kann es zu falschen Standardfehlern kommen.
Und zu niedrige Standardfehler bedeuten u.U. fälschlich niedrige p-Werte. Es wird also ein Testergebnis möglicherweise als signifikant ausgewiesen, auch wenn es das in Wahrheit gar nicht ist. Auch die Grenzen eines Konfidenzintervalls werden zu eng ausgegeben bei unterschätztem Standardfehler.
Genau gegen dieses Problem hilft Bootstrapping. Es wird für die Parameter je ein Standardfehler geschätzt ohne Rückgriff auf eine angenommene konkrete Verteilung. Und auch Konfidenzintervalle für die Regressionsparameter werden ohne Rückgriff auf Verteilungsannahmen konstruiert.
Gegen einen zu starken Einfluss von Ausreißern auf die Parameterschätzungen kann man sich mit Bootstrapping lediglich teilweise absichern. Mit Konfidenzintervallen auf Basis von Bootstrapping kann die überproportionale Wirkung einiger Ausreißer auf die Schätzungen zumindest transparent gemacht werden: Sie führt in so einem Fall in der Regel zu deutlich breiteren Konfidenzintervallen.
Dabei ist folgendes wichtig: Das Ziel von Bootstrapping ist nicht, bessere Schätzungen für die Parameter zu bekommen – die Parameterschätzungen unterscheiden sich i.d.R. nicht von gewöhnlichen Schätzverfahren (wie z.B. der Kleinst-Quadrate-Methode bei der Regression)! Das bedeutet auch, dass eine möglicherweise verzerrte Parameterschätzung aufgrund von Ausreißern durch Bootstrapping nicht behoben wird - es wird ggf. nur mittels größerer Standardfehler bzw. breiterer Konfidenzintervalle die Unsicherheit der Schätzung aufgrund der Ausreißer deutlicher gemacht. Als wirklich robustes Verfahren bezüglich Ausreißer würde ich eher eine sog. robuste Regression einsetzen, siehe Robuste Regression mit R .
Das Ziel ist vielmehr, bessere und robustere Schätzungen für die Streuung der Parameter zu bekommen. Und damit zuverlässige Signifikanztests und bessere Konfidenzintervalle.
4. Wie funktioniert Bootstrapping?
Um sich die Vorgehensweise bei dieser Methode zu veranschaulichen, ist zuerst eine kurze Wiederholung des normalen Vorgehens bei parametrischen Verfahren sinnvoll:
Wir ziehen eine Stichprobe (1) und das Statistikprogramm ermittelt aus dieser Stichprobe den gesuchten Parameter (z.B. ein Regressionsgewicht) und dessen Standardabweichung (2). Aus der Standardabweichung der Stichprobe berechnet das Progrmm den Standardfehler der Verteilung des Parameters. Unter der Annahme der Normalverteilung ergibt sich dann die sogenannte Stichprobenverteilung, also die Verteilung der Teststatistik (3). Aus dieser Teststatistik berechnen sich die Grenzen von Konfidenzintervallen bzw. kritische Werte für Parametertests (4).
Die folgende Grafik zeigt den Ablauf bei parametrischen Verfahren:
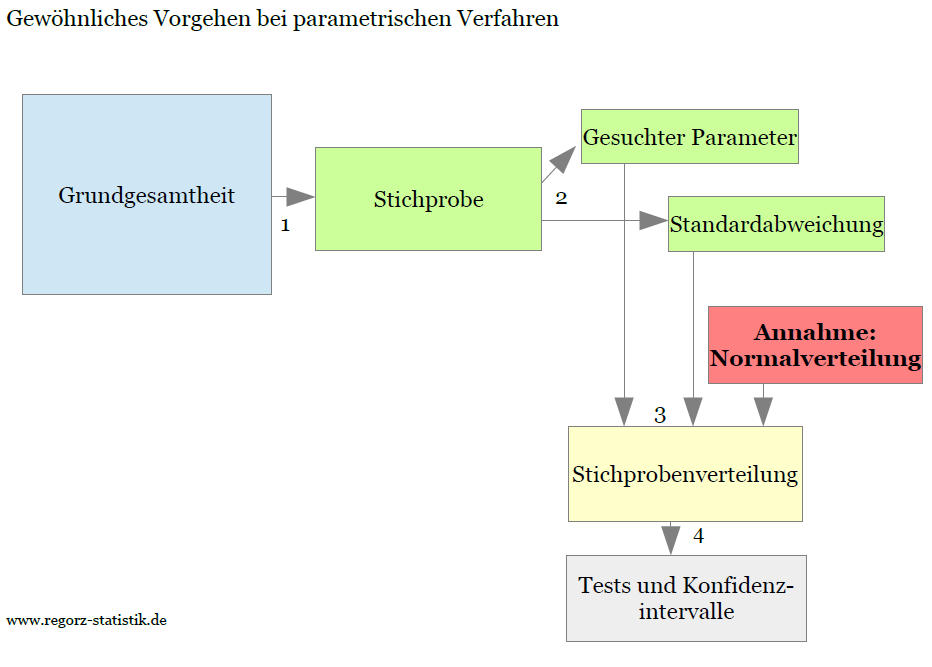
Beim Bootstrapping ist der Ablauf etwas anders:
Auch hier basiert das Verfahren auf einer Stichprobe (1). Diese Stichprobe wird jetzt jedoch als Ausgangsbasis für weitere Stichproben ("Bootstrap-Stichproben") genommen. Viele Male (z.B. 5000 Mal) wird aus der Stichprobe nach dem Modell mit Zurücklegen wiederum eine neue Stichprobe vom gleichen Umfang gezogen (2). Aus diesen vielen Bootstrap-Stichproben wird dann eine empirische Verteilung für die geschätzten Parameter ermittelt (3). Anhand dieser so gewonnenen Verteilung können dann Konfidenzintervalle und Standardfehler abgeleitet werden, ohne dass dafür Verteilungsannahmen notwendig sind (4).
Die folgende Grafik zeigt den Ablauf beim Bootstrapping:
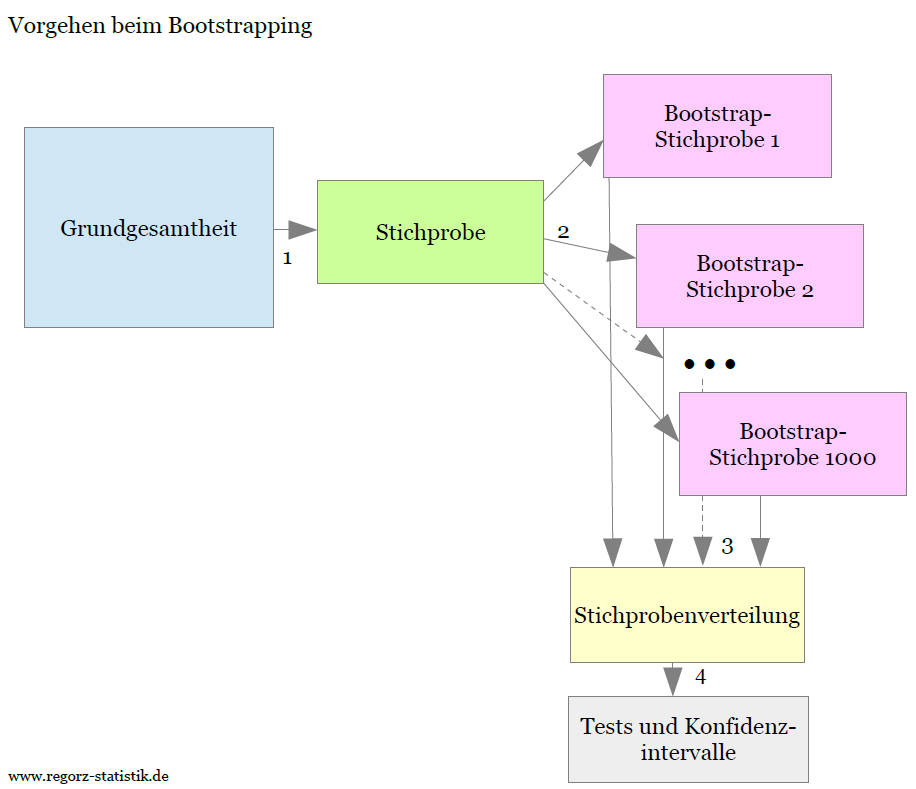
Das war jetzt noch etwas abstrakt erklärt, das folgende Beispiel soll es etwas plastischer machen.
5. Beispiel Bootstrapping
Die Funktionsweise des Verfahrens lässt sich an einer einfachen Regression gut demonstrieren. Für unser Beispiel nehmen wir eine Stichprobe vom Umfang n = 8. Das hat didaktische Gründe (Übersichtlichkeit), in der Realität braucht man größere Stichproben für Bootstrapping (siehe 5. Größe der Stichprobe)
Die ursprüngliche Stichprobe mit einem Prädiktor (= x) und einem Kriterium (= y), die aus irgendeiner Grundgesamtheit gezogen wurde, sei:
Stichprobe
| Nr. | Prädiktor (x) | Kriterium (y) |
|---|---|---|
| 1 | 4.6 | 9.5 |
| 2 | 5.3 | 10.1 |
| 3 | 3.9 | 8.6 |
| 4 | 4.7 | 9.5 |
| 5 | 4.3 | 7.4 |
| 6 | 3.7 | 7.4 |
| 7 | 5.1 | 9.2 |
| 8 | 6.0 | 14.6 |
Wenn man für die Stichprobe die Regressionsparameter bestimmt, ergibt sich b0 = - 2.77 und b1 = 2.62, wobei der Achsenabschnitt b0 nicht signifikant ist, die Steigung der Regressionsgeraden b1 jedoch schon (p = .005).
Aus dieser Stichprobe werden nun wiederum mit Zurücklegen Zufallsstichproben vom gleichen Umfang gezogen, also von n =8.
Bootstrap-Stichprobe 1
| Nr. | Prädiktor (x) | Kriterium (y) |
|---|---|---|
| 1 | 4.6 | 9.5 |
| 5 | 4.3 | 7.4 |
| 3 | 3.9 | 8.6 |
| 4 | 4.7 | 9.5 |
| 6 | 3.7 | 7.4 |
| 2 | 5.3 | 10.1 |
| 5 | 4.3 | 7.4 |
| 5 | 4.3 | 7.4 |
Sie sehen, dass ein Datensatz mehrfach gezogen wurde (5), andere dafür gar nicht (7, 8). Wenn man aus diesen Daten die Regressionsparameter bestimmt, erhält man b0 = 0.76 und b1 = 1.75.
Bootstrap-Stichprobe 2
| Nr. | Prädiktor (x) | Kriterium (y) |
|---|---|---|
| 1 | 4.6 | 9.5 |
| 8 | 6.0 | 14.6 |
| 5 | 4.3 | 7.4 |
| 3 | 3.9 | 8.6 |
| 3 | 3.9 | 8.6 |
| 3 | 3.9 | 8.6 |
| 4 | 4.7 | 9.5 |
| 7 | 5.1 | 9.2 |
Auch hier sind als Ergebnis der zufälligen Auswahl wieder Datensätze mehrfach, andere gar nicht enthalten. Wenn man aus diesen Daten die Regressionsparameter bestimmt, erhält man b0 = - 2.01 und b1 = 2.53.
Bootstrap-Stichprobe 3
| Nr. | Prädiktor (x) | Kriterium (y) |
|---|---|---|
| 2 | 5.3 | 10.1 |
| 4 | 4.7 | 9.5 |
| 6 | 3.7 | 7.4 |
| 8 | 6.0 | 14.6 |
| 8 | 6.0 | 14.6 |
| 2 | 5.3 | 10.1 |
| 5 | 4.3 | 7.4 |
| 5 | 4.3 | 7.4 |
Hierfür ergeben sich Regressionsparameter von b0 = - 6.45 und b1 = 3.35.
Diesen Vorgang wiederholt man noch z.B. 997 Mal, so dass am Ende 1000 Mal eine Stichprobe mit Zurücklegen aus der ursprünglichen Stichprobe gezogen worden ist und für jede dieser 1000 Stichproben die Parameter der Regression geschätzt wurden. (In seltenen Fällen kann es vorkommen, wenn für vereinzelte Bootstrap-Stichproben keine Schätzung möglich war und man daher eine Warnmeldung bekommt, dass z.B. nur 981 Stichproben berechnet werden konnte u.ä. Das sollte man dann auch so berichten.)
Mit diesen Daten erhält man eine empirische Verteilung der Schätzungen für die unterschiedlichen Parameter, hier für b0 und b1. Aus dieser Verteilung kann man für jeden Parameter den Standardfehler schätzen und auch jeweils ein Konfidenzintervall bestimmen – das macht der Computer (mit SPSS oder R) zum Glück automatisch. Bei größeren Modellen kann das jedoch durchaus einige Minuten dauern.
Zum Beispiel weist bei meiner Berechnung der Parameter b1 folgendes BCa-Konfidenzintervall (95%) auf: [0.86, 3.89]. Da dieses Intervall den Wert 0 nicht umschließt, spricht es für ein signifikantes Ergebnis.
Ich habe hier „bei meiner Berechnung“ geschrieben, weil die 1000 Stichproben per Zufallsziehung zu Stande kommen. Wenn Sie mit den gleichen Daten genau die gleiche Auswertung machen würden (oder wenn ich die Auswertung noch einmal starten würde), kämen nicht unbedingt exakt die gleichen Werte heraus – jede Bootstrap-Berechnung ist sozusagen ein Einzelstück.
Bei ausreichend großer Anzahl an Stichproben sind die Unterschiede zwischen verschiedenen Reihen von Ziehungen aber nur sehr gering.
6. BCa-Konfidenzintervalle
Es gibt verschiedene Verfahren des Bootstrapping. Das einfachste basiert auf per Bootstrap ermittelten Quantilen. Dieses Vorgehen hat jedoch in bestimmten Situationen unvorteilhafte Eigenschaften.
In der Praxis verbreitet ist das BCa-Verfahren. Diese Abkürzung steht für „Bias-corrected and accelerated“. Damit werden zwei potentielle Probleme bei anderen Bootstrap-Konfidenzintervallen abgefangen:
Bias bedeutet: Die Bootstrap-Stichprobenverteilung hat nicht zwingend den gleichen Mittelwert (genauer gesagt: Median) wie die gezogene Stichprobe. So kann es vorkommen, dass z.B. der Median der erhobenen Daten bei 10.0 ist, aber der aus diesen Daten über tausende Ziehungen zufällig ermittelte Median der Bootstrap-Ziehungen liegt bei 10.1. Die Differenz zwischen diesen beiden Werten ist der Bias, und der wird beim BCa-Verfahren automatisch korrigiert. Das Konfidenzintervall wird also in jedem Fall um den Median der gesamten Stichprobendaten gelegt.
Accelerated steht für eine Anpassung des Konfidenzintervalls insbesondere bei schiefen Verteilungen. Dort wird ohne Anpassung sonst das Konfidenzintervall eher zu eng gewählt, die Häufigkeit extremer Werte also unterschätzt.
Das BCa-Verfahren ist in SPSS als eine Option implementiert und sollte normalerweise gewählt werden.
7. Größe der Stichprobe
Auch wenn das Bootstrapping-Verfahren keine Annahmen über die zugrunde liegende Verteilung trifft, ist es nicht völlig ohne Voraussetzungen. Nur mit einer gewissen Mindestgröße der Stichprobe führt es zu vernünftigen Schätzungen. Eine Faustregel von Chernick (2008) dafür ist eine Stichprobengröße von mindestens n = 50 (zitiert nach Wright, London, & Field, 2011).
Das Verfahren ist also eher für mittlere Stichprobenumfänge geeignet. Für sehr kleine sollte man es nicht einsetzen. Für sehr große ist es häufig aufgrund des Zentralen Grenzwertsatzes nicht notwendig, weil man dann von einer näherungsweisen Normalverteilung der Stichprobenverteilung ausgehen kann. (Eine Verwendung von Bootstrapping ist aber auch dort natürlich nicht verkehrt).
Aber insbesondere für ein n zwischen ca. 50 und ca. 500 - 1000 bietet es eine gute zusätzliche Absicherung der Ergebnisse einer Regression.
8. Aufruf Bootstrapping in SPSS
Sie müssen eine wichtige Vorab-Entscheidung für den Aufruf in SPSS treffen: Wie viele Bootstrapping-Stichproben werden gezogen?
Die Voreinstellung hierfür ist 1000. Das ist für einen ersten Überblick über die Daten auch sinnvoll. Für die endgültige Auswertung empfiehlt Hesterberg (2015) jedoch mindestens 10000 Durchgänge, auch wenn das dann etwas länger dauert.
Mit nachfolgenden Syntax können Sie Standardfehler und Konfidenzintervalle für eine multiple Regression mit Bootstrapping berechnen lassen. Dabei ist AV der Name der abhängigen Variable/des Kriteriums, UV1 – UV4 sind die Namen von in diesem Beispiel vier unabhängigen Variablen/Prädiktoren (das Verfahren funktioniert mit mehr oder weniger als diesen vier Prädiktoren aber genauso).
/*normale Regression für p-Werte und Modellparameterschätzungen*/
REGRESSION
/MISSING LISTWISE
/STATISTICS COEFF OUTS CI(95)
/CRITERIA=PIN(.05) POUT(.10)
/NOORIGIN
/DEPENDENT AV
/METHOD=ENTER UV1, UV2, UV3, UV4
/SCATTERPLOT=(*ZRESID ,*ZPRED).
/*eigentliches Bootstrapping*/
BOOTSTRAP
/SAMPLING METHOD=SIMPLE
/VARIABLES TARGET=AV INPUT= UV1, UV2, UV3, UV4
/CRITERIA CILEVEL=95 CITYPE=BCA NSAMPLES=1000
/MISSING USERMISSING=EXCLUDE.
Der Aufruf aus den SPSS-Menüs heraus wird hier erklärt:
Aufruf BCa-Bootstrapping bei Regressionen (pdf)
Es gibt noch eine wichtige Einschränkung beim Aufruf: Wenn Sie bei der Regression Ergebnisse (vorhergesagte Werte, Residuen etc.) speichern wollen, geht das nicht im gleichen Schritt mit Bootstrapping. Dafür müssten Sie dann die Regression noch ein zweites Mal ohne diese Sonderfunktionalität aufrufen.
9. Interpretation der SPSS-Auswertung
Mehrere Beispiele und Übungsaufgaben zur Interpretation der SPSS Auswertung mit Bootstrapping finden Sie in folgender pdf-Datei:
Beispiele und Übungsaufgaben Interpretation SPSS Auswertung Bootstrapping bei Regression (pdf)
10. Testergebnisse berichten
Die Ergebnisse einer Regression werden meistens in Tabellenform berichtet. Ein Beispiel für eine derartige Ergebnistabelle mit BCa-Konfidenzintervallen ist:
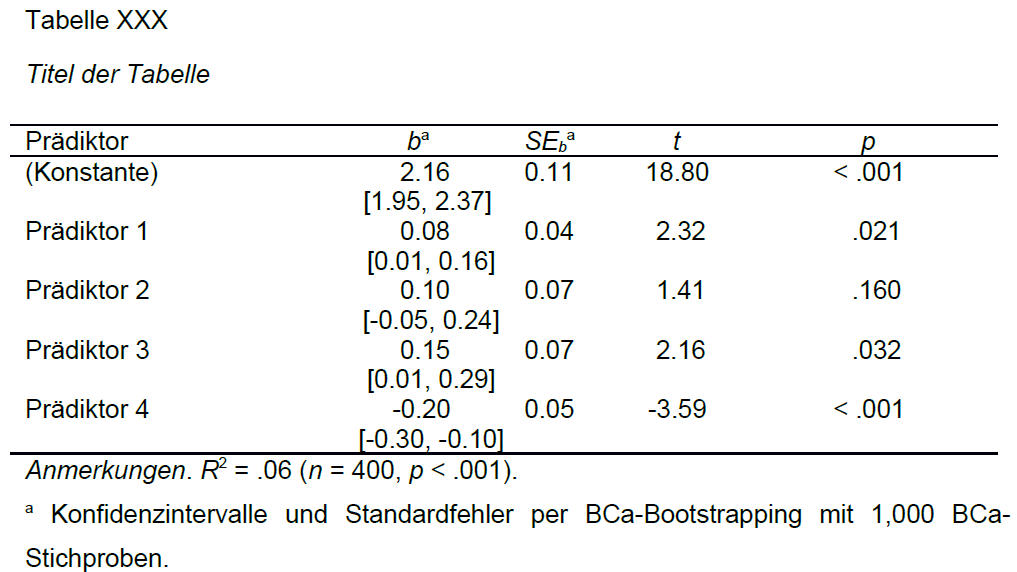
Es wird also in der Regel eine ganz normale Regressionstabelle berichtet. Je nach Fragestellung können auch noch weitere Spalten zu dieser Beispieltabelle hinzu kommen, z.B. die standardisierten Regressionsgewichte.
Es gibt nur zwei Besonderheiten:
- Die Konfidenzintervalle basieren auf Bootstrapping, ebenso die Standardfehler.
- Dieser Sachverhalt wird mit einer Fußnote berichtet, in der auch das Verfahren (empfohlen: BCa) und die Anzahl der Bootstrapping-Stichproben (hier: 1000) berichtet werden.
Natürlich würden Sie in einem realen Anwendungsfall statt der generischen Variablennamen (Prädiktor 1, Prädiktor 2 etc.) die inhaltlichen Namen aus Ihrem Modell berichten (z.B. „Einkommen“, „Geschlecht“ etc.). Und irgendwo im Text müsste generell bemerkt werden, dass es sich um 95%-Konfidenzintervalle handelt.
Im Verweis werden dann insbesondere die Konfidenzintervalle interpretiert. Bei diesen ist die entscheidende Frage, ob sie den Wert 0 einschließen, was gegen eine Signifikanz spricht, oder ob sie den Wert 0 nicht einschließen.
Ein möglicher Text zur o.g. Tabelle wäre:
„Die Ergebnisse dieser Analyse sind in Tabelle XXX aufgeführt. Mit Ausnahme von Prädiktor 2 waren in diesem Modell alle Prädiktoren signifikant. Insgesamt erklärt das Modell 6% der Varianz des Kriteriums. Die BCa-Konfidenzintervalle schlossen für alle signifikanten Prädiktoren den Wert Null nicht ein, so dass dieses Ergebnis robust war.“
11. Quellen
Field, A. (2013). Discovering statistics using IBM SPSS statistics: And sex and drugs and rock 'n' roll (4th edition). Los Angeles, CA: SAGE.
Hesterberg, T. C. (2015). What teachers should know about the bootstrap: Resampling in the undergraduate statistics curriculum. The American Statistician, 69, 371-386. doi: 10.1080/00031305.2015.1089789
Wright, D. B., London, K., & Field, A. P. (2011). Using bootstrap estimation and the plug-in principle for clinical psychology data. Journal of Experimental Psychopathology, 2, 252–270. doi:10.5127/jep.013611
Wie kann ich Sie weiter unterstützen?
Beratung für Datenauswertung bei Bachelorarbeit oder Masterarbeit
Welche Auswertungen sind für Ihre Fragestellung richtig und was müssen Sie dabei beachten? Schon in einer Stunde (Telefon/Skype/vor Ort) kann man viele Fragen klären. Auf meiner Seite zu Statistik-Beratung finden Sie weitere Informationen.