Robuste Standardfehler gegen Heteroskedastizität
Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, Stand: 05.09.2022
Eine wichtige Annahme bei der Regressionsanalyse ist die Homoskedastizität (Varianzhomogenität) der Regressionresiduen (also der Differenzen zwischen tatsächlichem Werten der AV und den durch die Regression geschätzten Werten). Wenn diese Regressionsvoraussetzung verletzt ist, dann können verzerrte Standardfehler und damit falsche Ergebnisse in Ihrem Hypothesentest die Folge sein. Näheres zur Voraussetzung der Homoskedastizität können Sie in meinem Tutorial Homoskedastizität als Regressionsvoraussetzung erfahren.
Eine der möglichen Lösungen bei verletzter Homoskedastizitätsannahme ist der Einsatz robuster Standardfehler, die auch bei Heteroskedastizität zu korrekten Ergebnissen führen. Diese nennt man heteroskedastizität-konsistente Standardfehler (im folgenden: HC-Standardfehler).
Inhalt
1. Auswahl des HC-Standardfehlers
Es sind verschiedene HC-Standardfehler entwickelt worden. Aktuell in Frage kommen vor allem die beiden Standardfehler HC3 und HC4, wobei HC4 Vorteile hat insbesondere in Situationen mit Verletzung der Normalverteilungsannahme oder mit Punkten mit großer Hebelwirkung (Hayes & Cai, 2007). Insofern würde ich im Zweifel HC4 als Standardfehler wählen. Falls Sie jedoch mit einem Programm arbeiten, das HC4 nicht implementiert hat, ist auch HC3 in der Regel eine gute Wahl.
2. Robuste Standardfehler in R
(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)
3. Robuste Standardfehler in SPSS
Nehmen wir das Beispiel einer Regression mit zwei Prädiktoren, uv1 und uv2, und eine Kriterium, av. Als Ergebnis einer gewöhnlichen multiplen Regression (ohne Berücksichtigung von Heteroskedastizität) könnte folgende Tabelle herauskommen:
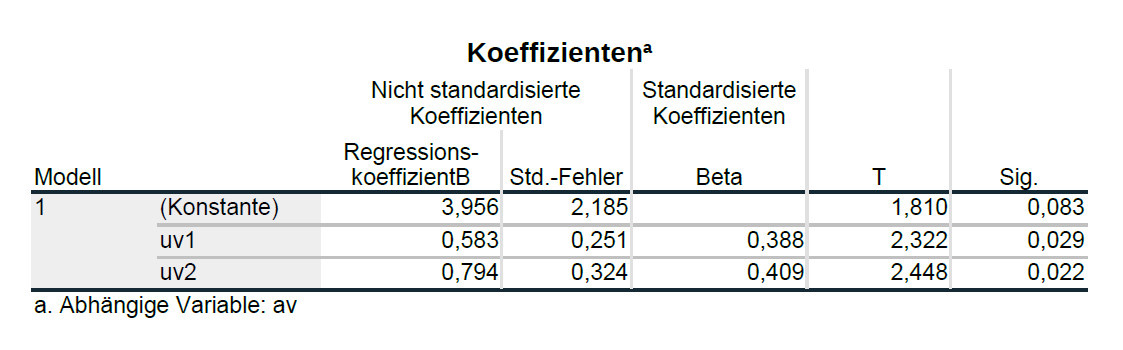
Wie bekommen Sie jetzt Regressionsergebnisse, die für den Einfluss von Heteroskedastizität korrigiert sind?
Leider kann man nun HC-Standardfehler nicht direkt im Regressionsdialog in SPSS (Vs. 25) aufrufen. Stattdessen kann man diese über den Menüpunkt „Allgemeines lineares Modell“ erhalten. Da diese Funktion recht mächtig und mitunter verwirrend von den Eingabemöglichkeiten im Menü her ist, würde ich sie eher über eine SPSS-Syntax aufrufen. Dabei müssen Sie lediglich Ihre eigenen Variablennamen für av, uv1 und uv2 unten ersetzen (und es funktioniert auch mit lediglilch einer oder ebenfalls mit mehr als zwei unabhängigen Variablen):
UNIANOVA av WITH uv1 uv2
/METHOD=SSTYPE(3)
/INTERCEPT=INCLUDE
/PRINT PARAMETER
/CRITERIA=ALPHA(.05)
/ROBUST=HC4
/DESIGN=uv1 uv2.
Bei der Option /ROBUST in der vorletzten Zeile können Sie statt HC4 auch einen der folgenden anderen HC-Standardfehler eintragen: HC0, HC1, HC2, HC3.
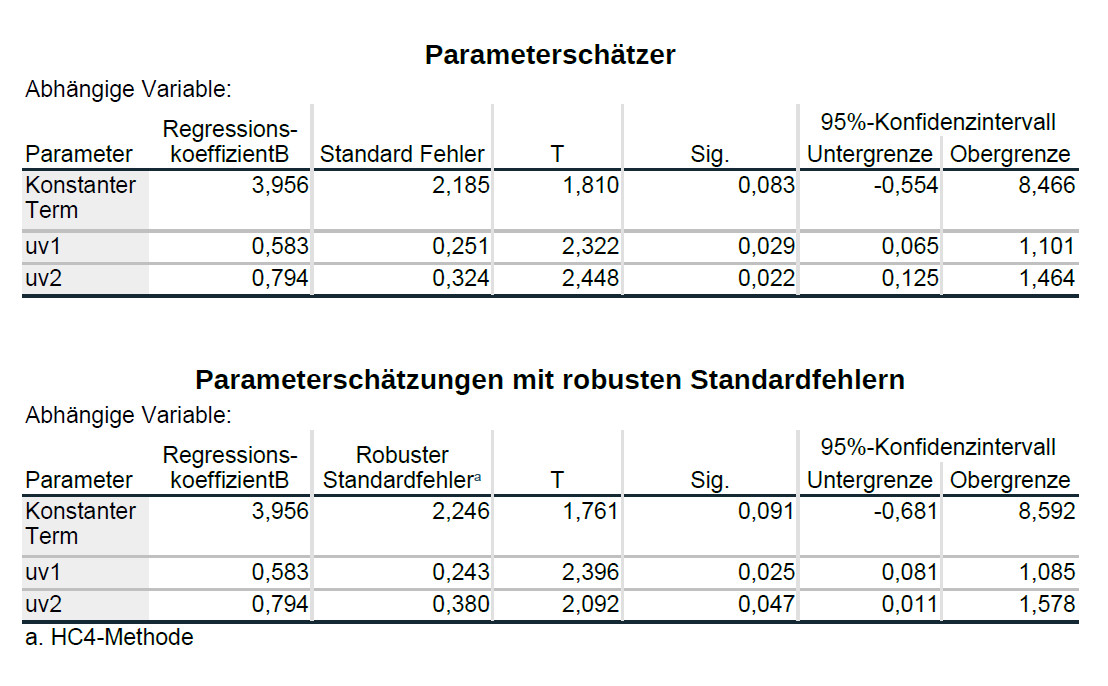
Über dem Ergebnis, das Sie dann bekommen, steht dann zwar „Univariate Varianzanalyse“, aber die Tabelle „Parameterschätzer“ ist inhaltlich das Gleiche wie die Tabelle „Koeffizienten“ Ihrer Regression, nur dass nun die standardisierten Betas fehlt, dafür jedoch automatisch Konfidenzintervalle für die Regressionsgewichte angegeben werden.
Die entscheidenden zusätzlichen Informationen stehen in der Folgetabelle, „Parameterschätzungen mit robusten Standardfehlern“. Hier sind für Standardfehler, t-Statistik, p-Wert und Konfidenzintervall die Werte auf Basis robuster Standardfehler berechnet worden, und diese Werte berichten Sie dann bei Vorliegen von Heteroskedastizität.
4. Quellen
Hayes, A. F., & Cai, L. (2007). Using heteroskedasticity-consistent standard error estimators in OLS regression: An introduction and software implementation. Behavior research methods, 39, 709-722. doi:10.3758/BF03192961
Long, J. S., & Ervin, L. H. (2000). Using heteroscedasticity consistent standard errors in the linear regression model. The American Statistician, 54, 217-224. doi:10.1080/00031305.2000.10474549
Wie kann ich Sie weiter unterstützen?
Beratung für Datenauswertung bei Bachelorarbeit oder Masterarbeit
Welche Auswertungen sind für Ihre Fragestellung richtig und was müssen Sie dabei beachten? Schon in einer Stunde (Telefon/Skype/vor Ort) kann man viele Fragen klären. Auf meiner Seite zu Statistik-Beratung finden Sie weitere Informationen.