Mehrebenenanalyse (HLM) mit R:
4. Random Effects auf Signifikanz prüfen

Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, 21.08.2023

Wenn Sie im Rahmen einer Mehrebenenanalyse (oder HLM oder linear mixed effects model – im Folgenden werden diese Begriffe austauschbar verwendet) Random Effects berücksichtigen, möchten Sie in der Regel auch prüfen, ob sich diese signifikant von Null unterscheiden. Dieses Tutorial zeigt am Beispiel des lme4-Moduls von R, wie das funktioniert.

Die Berechnungen beruhen auf einem Beispieldatensatz von Hox für das 2. Kapitel des Buchs von Hox et al. (2017). Der Datensatz kann bei Hox (http://joophox.net/mlbook2/DataExchange.zip) heruntergeladen werden.

INHALT

  1. Grundlagen
  2. Beispiel Signifikanztest Random Slope in R
  3. Vollständiger R-Code mit lme4 Package
  4. Vollständiger R-Code mit nlme Package
  5. Literatur

1. Grundlagen

Für die Fixed Effects erhält man in lme4 bei der zusätzlichen Verwendung des Moduls lmerTest automatisch p-values. Aber wie bekommt man p-values für Random Effects in R?

Im hier vorgestellten Ansatz wird im Rahmen des Hierarchical Linear Modeling die Deviance (bzw. dessen REML-Gegenstück) zwischen verschiedenen genesteten Modellen miteinander verglichen. Wie im Grundlagentutorial geschildert, ist die Deviance ein relatives Maß für die Modellgüte, die man zum Vergleich von genesteten Modellen verwenden kann. Die Differenz der Deviance folgt einer Chi-Quadrat-Verteilung mit so vielen Freiheitsgraden, wie in dem umfassenderen Modell zusätzliche Parameter geschätzt wurden.

Dabei gibt es jedoch drei Herausforderungen, die man bei der Lösung beachten muss:

  • Bei einer Random Slope geht es um eine Zufallskomponente. Um Zufallskomponenten korrekt schätzen zu können, muss man die REML-Schätzung (restricted maximum likelihood) verwenden, und zwar hier für beide Modelle, die man miteinander vergleichen möchte.
  • Häufig wird bei Hinzunahme einer Random Slope gleichzeitig auch eine Random Kovarianz zwischen Slope und Intercept geschätzt, beispielsweise wenn man für den Zufallsterm in lme4 die Schreibweise (1 + slope|gruppe) verwenden würde. Das macht es aber nicht möglich, im Modellvergleich die Signifikanz der Random Slope zu bestimmen, da jetzt das Modell mit Random Slope zusätzlich auch noch eine Random Kovarianz enthielte, und man nur den zusätzlichen Erklärungsbeitrag beider Zufallseffekte zusammen auf das Modell auf Signifikanz prüfen könnte. Daher muss zuerst ein Modell nur mit Random Slope (ohne Random Kovarianz) geschätzt werden.
  • Eine Varianz ist als quadrierte Größe theoretisch immer positiv. Damit kann sie auch nur in eine Richtung von Null abweichen. Das ist anders als bei den Fixed Effects und auch bei einer Random Kovarianz, die in beide Richtungen von der Null abweichen können. Das führt dazu, dass ein Chi-Quadrat-Test (LR-Test) zu konservativ ist und daher der p-Wert im Nachhinein noch angepasst werden muss.

2. Beispiel Signifikanztest Random Slope in R

Dieses Beispiel beruht auf den Modellschätzungen aus dem Tutorial Mehrebenenanalyse mit R (HLM mit R): lme4 Package, dort wird der jeweilige Code ausführlich erklärt. Als Packages wurden im Folgenden verwendet:

library(lme4)
library(lmerTest)

Nachdem dort die Schätzung einer Random Slope für das Geschlecht zu Schätzproblemen geführt hatte, wird hier nur eine Random Slope für die Extraversion der Schülerinnen und Schüler geschätzt. Für die Auswirkungen dieser Random Slope vergleichen wir zunächst ein Modell mit Fixed Slopes (auf Level 1 für Geschlecht und Extraversion der Schülerinnen und Schüler sowie als Level 2 Prädiktor Berufserfahrung der Lehrkraft) mit einem Modell mit zusätzlich einer Random Slope für die Extraversion der Schülerinnen und Schüler.

Wie oben ausgeführt, müssen wir diese Schätzung für beide zu vergleichende Modelle mit REML durchführen (wenn Sie das Modell für die Fixed Effects in einem vorherigen Schritt mit ML geschätzt haben, müssen Sie jetzt diese Schätzung mit REML wiederholen).

Bei der Schätzung des Modells mit Random Slope ist zu beachten, dass Sie hier zunächst nur eine Random Slope schätzen, keine zusätzliche Random Kovarianz. Das heißt, die einfache Schätzung des Zufallseffekts mit (1+extrav|class) geht nicht, da bei beiden Zufallseffekten (Intercept: 1, Slope: extrav) in einer Klammer automatisch auch eine Random Kovarianz geschätzt würde. Stattdessen müssen in lme4 jetzt zwei Zufallseffekte angegeben werden: (1|class) für den Random Intercept und (0+extrav|class) für die Random Slope ohne Interceptschätzung.

Die Aufrufe der beiden Modelle ist:

# Fixed Slopes (Random intercept)

fixed_slopes <- lmer(popular ~ 1 + sex + extrav + texp +
(1|class), data=popular2, REML=TRUE)
summary(fixed_slopes)

# Random Slopes nur Extraversion

random_slope <- lmer(popular ~ 1 + sex + extrav + texp +
(1|class)+(0+extrav|class), data=popular2, REML=TRUE)
summary(random_slope)

Unter dem Label "REML criterion at convergence:" findet man jetzt im Output das Äquivalent zur Deviance bei einer REML Schätzung für beide Modelle.

Diese beiden Werte kann man nun mit der anova-Funktion über einen LR-Test miteinander vergleichen. Dabei ist es wichtig, den Parameter "refit = FALSE" zu setzen, da sonst das Modell nochmals mit ML geschätzt wird, was wir hier ausdrücklich nicht möchten.

anova(fixed_slopes, random_slope, refit = FALSE)

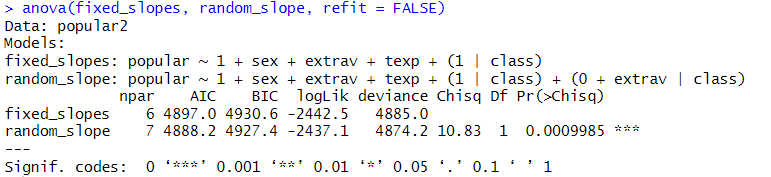
Grafik REML intercept und slope


Den sich hier ergebenden p-Wert von .0009985 müssen Sie noch durch 2 teilen, aus den in der Einleitung angegebenen Gründen. Damit ergibt sich ein p-Wert von .0004993, wir haben also eine signifikante Random Slope von Extraversion, das heißt der Einfluss von Extraversion auf die Popularität unterscheidet sich signifikant zwischen den Schulklassen.

In einem zweiten Schritt können Sie jetzt noch prüfen, ob es auch eine Random Kovarianz zwischen Intercept und Slope gibt. Dazu schätzen Sie das entsprechende Modell:

# Random Kovarianz

random_kovarianz <- lmer(popular ~ 1 + sex + extrav + texp +
(1+extrav|class), data=popular2, REML=TRUE)
summary(random_kovarianz)

anova(random_slope, random_kovarianz, refit = FALSE)

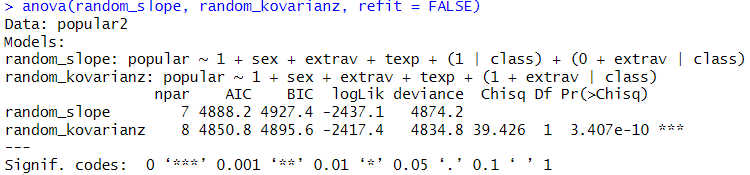
Grafik REML slope und covariance


Für die Random Kovarianz ergibt sich ein p-Wert von 3.407e-10. Dieser darf nicht durch 2 geteilt werden, da eine Kovarianz in beide Richtungen von der Null abweichen kann. Wir haben hier also eine signifikante Random Kovarianz, es gibt also einen signifikanten Zusammenhang in der Abweichung des Gruppen-Intercept vom Fixed Intercept zur Abweichung des Gruppen-Slope vom Fixed Slope für Extraversion.

3. Vollständiger R-Code mit lme4 Package

library(lme4)
library(lmerTest)
head(popular2, 5)

# Fixed Slopes (Random Intercept)

fixed_slopes <- lmer(popular ~ 1 + sex + extrav + texp +
(1|class), data=popular2, REML=TRUE)
summary(fixed_slopes)

# Random Slopes nur Extraversion

random_slope <- lmer(popular ~ 1 + sex + extrav + texp +
(1|class)+(0+extrav|class), data=popular2, REML=TRUE)
summary(random_slope)

anova(fixed_slopes, random_slope, refit = FALSE)
# Ergebnis noch durch 2 teilen!

# Random Kovarianz

random_kovarianz <- lmer(popular ~ 1 + sex + extrav + texp +
(1+extrav|class), data=popular2, REML=TRUE)
summary(random_kovarianz)

anova(random_slope, random_kovarianz, refit = FALSE)

4. Vollständiger R-Code mit nlme Package

library(nlme)

# Fixed Slopes (Random Intercept)

fixed_slopes_nlme <- lme(popular ~ 1 + sex + extrav + texp,
data=popular2, random = ~1 |class,
method="REML")
summary(fixed_slopes_nlme)

# Random Slope (No Random Covariance)

random_slope_nlme <- lme(popular ~ 1 + sex + extrav + texp,
data=popular2,
random = list(class = pdDiag(~ extrav)),
method="REML")
summary(random_slope_nlme)

# Werte aus dem Output abgelesen unter "logLik"
0.5 * pchisq(-2*(2437.097-2442.512), 1, lower.tail = FALSE)

# Random Slope & Random Covariance

random_covariance_nlme <- lme(popular ~ 1 + sex + extrav + texp,
data=popular2,
random= ~ extrav |class,
method="REML")
summary(random_covariance_nlme)

# Werte aus dem Output abgelesen unter "logLik"
pchisq(-2*(2417.384-2437.097), 1, lower.tail = FALSE)

5. Literatur

Hox, J. J., Moerbeek, M., & Van de Schoot, R. (2017). Multilevel analysis: Techniques and applications (3rd edition). Routledge.


Weitere Tutorials zur Mehrebenenanalyse/HLM mit R: