Mehrebenenanalyse mit R (HLM mit R)
– lme4 Package

Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, 05.11.2024

Das wohl beliebteste Modul für Mehrebenenanalysen (= Hierarchische lineare Modelle, HLM) in R ist lme4. Mit diesem Package ist es vergleichsweise einfach, ein hierarchisches lineares Modell mit R aufzustellen und zu analysieren.

Es gibt allerdings bestimmte Datenkonstellationen, z.B. Längsschnittmodelle mit korrelierten Fehlern (u.a. aufgrund von Erinnerungseffekten), bei denen lme4 an seine Grenzen kommt. Dann kann der Einsatz eines anderen R-Moduls sinnvoll sein, nlme - siehe dazu mein Tutorial Linear Mixed Effects Model mit R (Längsschnitt).

INHALT

1. Nullmodell
2. Fixed Slopes (Random Intercept)
3. Random Slopes
4. Cross-Level-Interaction
5. Vollständiger R-Code
6. Ausblick
7. Literatur

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

Bei der Mehrebenenanalyse erfolgt die Modellierung üblicherweise in mehreren Schritten. Man startet in der Regel mit dem einfachsten möglichen Modell, dem Nullmodell, erweitert dieses um Fixed Slopes, später um Random Slopes und ggf. noch um Cross Level Interactions.

Zu Beginn müssen wir, wie immer bei R, relevante Packages laden (bzw. vorab mit install.packages einmalig installieren, wenn Sie diese noch nie verwendet haben):

library(lme4)
library(lmerTest)
library(performance)
library(reghelper)

Dabei ist lme4 der Name des eigentlichen HLM-Moduls, während lmerTest eine Ergänzung dafür ist, um für die Fixed Effects auch p-Werte zu erhalten. Das Modul performance erleichtert uns die Berechnung der ICC (Intraklassenkorrelation). Das Modul reghelper dient der Darstellung der sogenannten Simple Slopes für das Modell mit Cross-Level-Interaction.

Wir wollen eine Mehrebenenanalyse mit einem Datensatz demonstrieren, der aus dem Buch von Hox et al. (2017) stammt und dort im Kapitel 2 vorgestellt wird. Sie können sich diesen Datensatz auf der Internetseite von Hox herunterladen (http://joophox.net/mlbook2/DataExchange.zip). Generell ist das Buch von Hox et al. sehr empfehlenswert, wenn man sich intensiver mit HLM auseinandersetzen will oder muss, insbesondere die Kapitel 2-4, 12-13.

Mit diesem Datensatz wollen wir untersuchen, wovon die Popularität von Schülerinnen und Schülern (genestet in verschiedenen Schulklassen) abhängt. Auf der Ebene der Schülerinnen und Schüler (Level 1) sind dabei als Prädiktoren das Geschlecht (0 = m, 1 = w) enthalten sowie deren Extraversion. Auf der Ebene der Schulklassen (Level 2) ist als Prädiktor die Berufserfahrung der Lehrkraft (in Jahren) relevant. Diese Variable ist auf Ebene 2, weil alle Schülerinnen und Schüler einer Klasse dieselbe Lehrkraft haben und damit denselben Wert auf dieser Variable.

Hinweis: Bei der folgenden Modellierung wurde aus didaktischen Gründen entsprechend des Beispiels aus dem Buch von Hox et al. (2017) keine Prädiktorvariable zentriert. Die Zentrierung von Prädiktoren ist im Rahmen von HLM ein wichtiges, aber auch komplexes Thema, so dass es zum Einstieg leichter ist, zunächst einmal ein Modell ohne Zentrierung zu schätzen. Zur Frage der verschiedenen Möglichkeiten der Zentrierung siehe das Tutorial Mehrebenenanalyse Zentrierung sowie bei Enders & Tofighi (2007). Außerdem wurde hier entsprechend dem Beispiel durchweg die ML-Schätzung verwendet, auch wenn in der Praxis für einige der Modelle eher die REML-Schätzung zu empfehlen wäre, siehe ML oder REML-Schätzung?

1. Nullmodell

Am Anfang steht in der Mehrebenenanalyse das Nullmodell. Das ist gar kein Modell im engeren Sinne, weil es gar nichts erklärt bzw. modelliert – es beschreibt nur das Ausmaß der Schwankung einerseits innerhalb der Gruppen und andererseits zwischen den Gruppen.

Damit ist das Nullmodell, also ein Modell nur mit Random Intercept, ein guter Ausgangspunkt, um die Erklärungsgüte weiterer Modellierungsschritte zu beurteilen. Gleichzeitig ist das Nullmodell die Basis, um in einer Mehrebenenanalyse die ICC (Intraklassenkorrelation) zu berechnen. In einem Mehrebenenmodell ist die ICC ein Maß dafür, wie ähnlich sich verschiedene L1-Untersuchungseinheiten einer L2-Einheit sind – in unserem Beispiel also, wie ähnlich sich verschiedene Schülerinnen und Schüler einer Klasse sind.

Hier ist der Aufruf der Modellschätzung des Nullmodells mit lme4:

nullmodell <- lmer(popular ~ 1 + (1|class), data=popular2, REML=F)
summary(nullmodell)

Wie wir sehen, erfolgt die Schätzung mit der lmer-Funktion. Diese ist für Mehrebenen-Analysen das Gegenstück zur normalen lm-Funktion bei der linearen Regression. Es werden hier drei Gruppen von Parametern übergeben:

Die eigentliche Modellformel lautet: popular ~ 1 + (1|class)

Der Name des verwendeten Datensatz wird hier angegeben: data=popular2

Die Einstellung des Schätzverfahrens erfolgt hier: REML = F

Wenn man REML auf False setzt, erfolgt die Schätzung mit einem Maximum Likelihood (ML) Schätzer, was den Vorteil hat, dass man mit der sog. Deviance Modellvergleiche durchführen kann; die Alternative mit REML auf True wäre die sog. Restricted ML-Schätzung. Weitere Informationen zu den beiden Schätzverfahren, ML und REML, finden Sie u.a. bei Hox et al. (2017).

Jetzt zur eigentlichen Modellformel: Bei einem HLM-Modell besteht diese aus drei Teilen:

• Der abhängigen Variable, gefolgt von einer Tilde - hier: popular ~
• Den Fixed Effects - hier: 1 (=Schätzung des Intercepts)
• Den Random Effects in der Klammer mit Angabe der Gruppierungsvariable - hier: + (1|class)

Fixed Effects sind im Rahmen der HLM Effekte, die über alle Gruppen (Level 2 Einheiten) hinweg geschätzt werden. Random Effects hingegen sind Effekte, die sich zwischen den Gruppen unterscheiden.

Der Fixed Effect in unserem Beispiel, 1, ist ein Intercept, also der bekannte Achsenabschnitt einer Regressionsgleichung. Da wir im Nullmodell noch gar keine Slopes, also noch keine Regressionsgeraden haben, ist der Fixed Intercept hier eine Schätzung für die erwartete mittlere Ausprägung der abhängigen Variablen. Hier im Beispiel ist es also die erwartete Popularität eines zufällig gewählten Schülers bzw. Schülerin aus einer zufällig ausgewählten Klasse. Für die späteren Folgemodelle mit Slopes ist der Fixed Intercept aber dann ein echter Intercept. Dann ist es also der Effekt, wenn alle Prädiktoren eine Ausprägung von Null haben.

Der Random Effect in unserem Beispiel, (1|class), bedeutet, dass der Intercept (dargestellt durch die 1), zwischen den Level 2 Einheiten, also hier den Schulklassen, schwankt. (1|class) lässt sich also so übersetzen: Ermittele, wie stark die Schwankung des Intercepts (und im Nullmodell damit des Mittelwertes) zwischen den verschiedenen Schulklassen ist.

In unserem Schulbeispiel sind Fixed Effects die Effekte, die alle Schülerinnen und Schüler betreffen. Die Random Effects hingegen zeigen das Ausmaß der Schwankungen in den Effekten zwischen den verschiedenen Schulklassen an. Wenn man einen Random Effect in das Mehrebenenmodell aufnimmt, dann eigentlich immer zusammen mit dem dazugehörigen Fixed Effect – umgekehrt gilt das nicht, man kann also durchaus einen Fixed Effect im Modell haben ohne dazugehörigen Random Effect (wenn nämlich dieser Effekt zwischen den Klassen nicht schwankt, sondern in allen Klassen ungefähr gleich stark ausfällt).

Wenn wir diesen R-Code mit unseren Beispieldaten ausführen, erhalten wir folgenden Output:

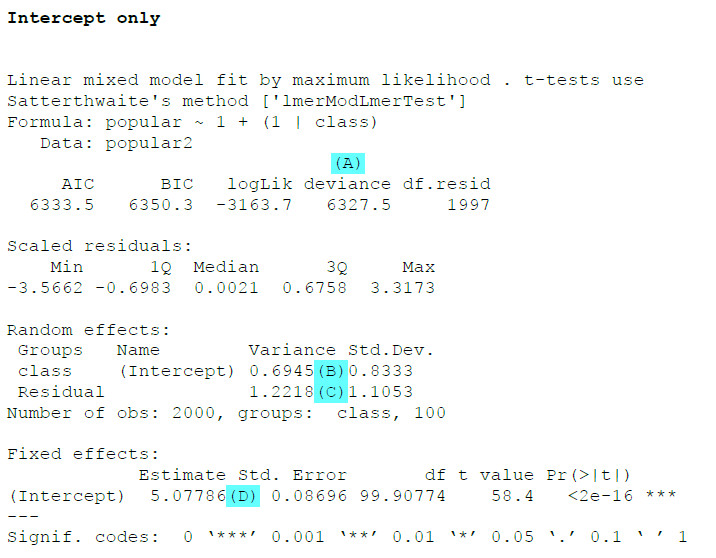
Zunächst einmal ist es wichtig, dass wir keine Fehlermeldung bekommen haben – gerade später bei den komplexeren Modellen mit Random Slopes kann es nämlich durchaus passieren, dass das Programm keine gültige Schätzung vornehmen konnte.

Die wichtigsten Informationen aus dem Output:

(A): Im Hierarchical Linear Model ist die Deviance ein Maß für die Modellgüte. Dabei ist eine kleinere Deviance besser als eine größere. Interessant ist dabei weniger der absolute Wert als der Vergleich mit einem anderen Modell (genauer gesagt: mit einem genesteten Modell, also einem Modell, das alle Elemente des Modells enthält und lediglich ein oder mehrere zusätzliche Parameter schätzt).

(B): Hier ist die Varianz für den Random Intercept angegeben und damit in diesem Nullmodell die Antwort auf die Frage, wie stark die Mittelwerte der Popularität der Gruppen (Schulklassen) um das Gesamtmittel schwanken. Meistens werden bei HLM die Varianzen berichtet, aber inhaltlich leichter interpretierbar ist die dazugehörige Standardabweichung (SD).

(C): Hier ist die Fehlervarianz angegeben, also die Varianz auf Level 1 des Mehrebenenmodells. Diese gibt an, wie stark im Durchschnitt die Popularität innerhalb einer Schulklasse um die mittlere Popularität in dieser Schulklasse schwankt.

(D): Dies ist der Fixed Intercept und damit hier (im Nullmodell) die erwartete durchschnittliche Popularität von zufällig ausgewähltem Schüler/Schülerin aus einer zufällig ausgewählten Klasse.

Aus den Werten (B) und (C) kann man zusätzlich noch die Intraklassenkorrelation (ICC) berechnen. Das geht am einfachsten mit folgendem Befehl (auf Basis des Moduls performance):

icc(nullmodell)

Das relevante Ergebnis ist die „Adjusted ICC“.

Alternativ kann man die ICC auch per Hand berechnen. Man teilt die Varianz des Random Intercept durch die Summe der Varianz von Random Intercept und der Fehlervarianz, also in unserem Beispiel:

ICC = 0.6945 / (0.6945 + 1.2218) = .362.

Inhaltlich beschreibt die ICC, wie groß der Anteil an der Gesamtvarianz ist, der von höheren Ebenen (hier von den Schulklassen) ausgeht.

2. Fixed Slopes (Random Intercept) mit lme4

Das erste echte Modell, das also etwas erklärt, ist ein Modell mit Fixed Slopes, das heißt mit Regressionsgewichten, die für alle Gruppen (hier: Schulklassen) gleich sind. In unserem Beispiel gibt es gleich drei Fixed Slopes: Extraversion (extrav), Geschlecht (sex) und Berufserfahrung der Lehrkraft (texp).

Dabei ist zu beachten, dass Extraversion und Geschlecht Effekte auf Level 1 sind, weil sich die Schülerinnen und Schüler hinsichtlich Extraversion und Geschlecht unterscheiden. Die Berufserfahrung der Lehrkraft hingegen ist ein Level 2 Prädiktor, weil alle Schülerinnen und Schüler in einer konkreten Schulklasse die gleiche Lehrkraft haben. Für einen solchen Level 2 Effekt kann es insofern auch später keine Random Slopes geben, die gibt es generell nicht für die höchste Ebene im Modell (in unserem Beispiel also nicht für Level 2).

Im Buch von Hox ist dieses Modell nicht abgedruckt, dennoch ist es m.E. empfehlenswert, diesen Schritt einzuschieben.

Hier ist der Aufruf der Modellschätzung für ein Fixed Slope Model in der lmer Funktion:

fixed_slopes <- lmer(popular ~ 1 + sex + extrav + texp + (1|class), data=popular2, REML=F)
summary(fixed_slopes)

Der einzige inhaltliche Unterschied zum vorherigen Modell (Nullmodell) ist die Schätzung der Fixed Effects:

1 + sex + extrav + texp

Dieser Befehl bedeutet, dass wie bisher ein Intercept (1) geschätzt werden soll und zusätzlich Fixed Effects (= Regressionsgewichte) für die Variablen sex (binäre Variable), extrav und als Level 2 Prädiktor texp.

Als Output erhalten wir auf der Basis des Beispieldatensatzes:

Hier sind vor allem interessant:

(E): Die Deviance ist gegenüber dem vorherigen Modell zurückgegangen, von 6327.5 auf 4862.3, unser zweites Modell kann also die Zusammenhänge deutlich besser erklären als das Nullmodell.

(F): Hier sind wieder die Random Effects angegeben. Wir sehen im Vergleich zum Nullmodell, dass durch die Hinzunahme der drei Prädiktoren sowohl die Varianz des Intercepts (also die Varianz zwischen den Gruppen) als auch die Varianz innerhalb der Gruppen (Residual) zurückgegangen ist.

(G): Dies ist, über alle Klassen hinweg, der Effekt des Geschlechts. In der Spalte "Estimate" ist das Regressionsgewicht. Schülerinnen (sex =1) haben eine signifikant (Spalte "Pr(>|t|)") höhere Popularität als Schüler (sex =0).

(H): Extraversion der Schülerinnen und Schüler hat einen signifikant positiven Effekt auf die Popularität.

(I): Die Berufserfahrung der Lehrkraft hat ebenfalls einen positiven Effekt auf die Popularität – in Klassen mit erfahrenen Lehrkräften sind die Schülerinnen und Schüler populärer (unter Kontrolle von Geschlecht und Extraversion - wie bei der multiplen Regression sind alle Effekte unter Kontrolle der jeweils anderen Prädiktoren).

3. Random Slope Model mit lme4

Im nächsten Schritt wollen wir prüfen, ob sich der Einfluss der beiden Level 1 Prädiktoren, also Geschlecht und Extraversion, zwischen den Schulklassen unterscheidet. Wir benötigen also ein Modell mit Random Slope und Random Intercept in R.

Hier ist ein Modell mit Random Slope in der lmer Funktion:

random_slopes <- lmer(popular ~ 1 + sex + extrav + texp + (1+sex+extrav|class),
data=popular2, REML=F)
summary(random_slopes)

Der inhaltliche Unterschied zur vorherigen Auswertung liegt in der Spezifikation der Random Effects:

(1+sex+extrav|class)

Das sagt aus, dass nun der Intercept sowie der Effekt des Geschlechts und der Effekt der Extraversion auf die Popularität zwischen den Schulklassen schwanken können. (Für die Level 2 Variable Berufserfahrung der Lehrkraft ist ja kein Random Effect möglich, da dies auf der obersten Modellebene nicht geht, s.o.)

Als Output erhalten wir:

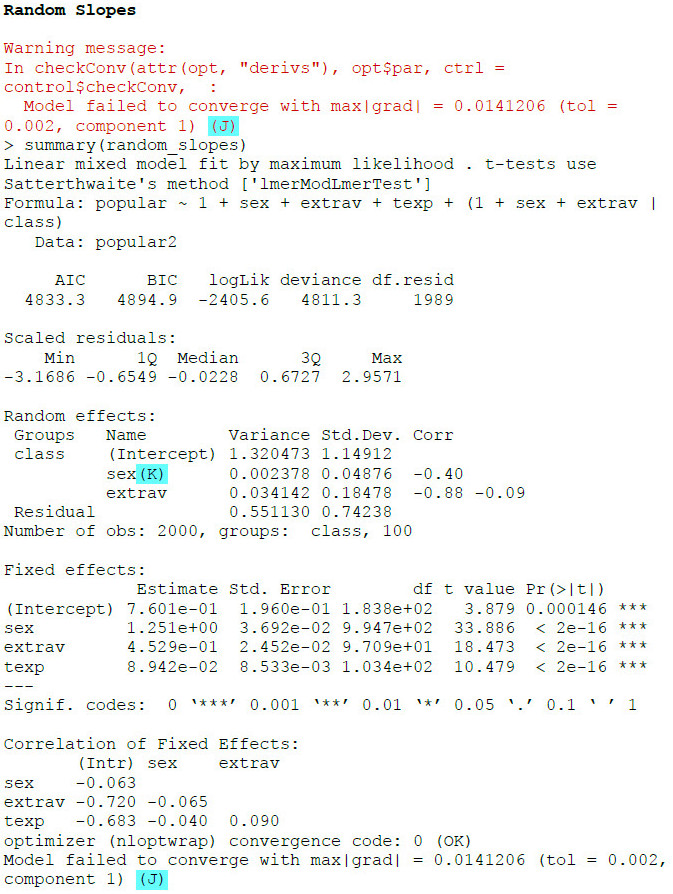
(J) Wir erhalten einen Warnhinweis, dass das Modell nicht konvergiert ist. Das Programm konnte also keine gültige Parameterschätzung vornehmen. Insofern können wir den Ergebnissen nicht trauen.

(K) Eine häufige Ursache für ein nicht konvergierendes Modell bei der Hinzunahme von Random Effects ist eine zu geringe Varianz für einen Random Effect – denn das führt zu Schätzproblemen. Hier sehen wir bei der Varianzschätzung für den Effekt des Geschlechts mit 0.002 einen sehr geringen Wert.

Insofern verändern wir jetzt unser Modell dahingehend, dass wir für das Geschlecht keine Random Slope mehr schätzen, sondern nur für die Extraversion:

random_slopes2 <- lmer(popular ~ 1 + sex + extrav + texp + (1+extrav|class),
data=popular2, REML=F)
summary(random_slopes2)

Die entscheidende Änderung ist wieder der Random Effect:

(1+extrav|class),

Jetzt wird nur für den Intercept und für die Extraversion ein Random Effect geschätzt, nicht mehr für Geschlecht.

Als Output erhalten wir:

Diesmal haben wir keinen Warnhinweis mehr, die Modellschätzung war also erfolgreich.

(L) Die Deviance ist weiter zurückgegangen, von 4862.3, auf 4812.8.

(M) Die Varianz der Random Slope für Extraversion beträgt 0.034, die Standardabweichung 0.18. Zum Vergleich: Die Fixed Slope für Extraversion beträgt 0.45 (siehe im Output unten unter „Fixed Effects“), wir sehen also eine deutliche Schwankung des Effekts der Extraversion zwischen den Klassen. Ob diese Schwankung signifikant ist, ist ein Spezialthema (siehe Tutorial Varianzkomponenten/Random Effects auf Signifikanz prüfen ).

(N) Wenn mehr als ein Random Effect geschätzt wird (die Schätzung des Level 1 Residuums ausgenommen), dann schätzt das Programm automatisch auch eine Kovarianz (in diesem Fall ausgewiesen als Korrelation) zwischen den Random Effects. Allerdings ist diese schwer zu interpretieren, da es hier um die verbleibende Kovarianz nach Berücksichtigung der verschiedenen Prädiktoren geht.

4. Cross Level Interaction mit lme4

Als letztes wollen wir noch eine Cross Level Interaction schätzen. Wir hatten unter 3. eine substantielle Varianz für die Random Slope der Extraversion gefunden, also eine Schwankung des Effekts der Extraversion auf die Popularität zwischen den Klassen. Wir wollen nun prüfen, ob der Effekt der Extraversion auf die Popularität der Schülerinnen und Schüler vielleicht (teilweise) von der Berufserfahrung der Lehrkraft abhängt. Das könnte die Schwankung dieses Effekts zwischen den Schulklassen erklären.

Dazu spezifizieren wir eine Cross Level Interaction zwischen der Level 1 Variable Extraversion und der Level 2 Variable Erfahrung der Lehrkraft. Im Prinzip ist das eine ganz normale Moderationsanalyse, nur mit dem Unterschied, dass UV und Moderator auf zwei verschiedenen Ebenen angesiedelt sind (es wäre aber prinzipiell auch möglich, im Rahmen von HLM Moderationen auf einer Ebene zu untersuchen, also z.B. zwischen zwei Level 1 Variablen).

Hier ist der R-Code für das Modell mit Cross Level Interaction in R:

cross_level <- lmer(popular ~ 1 + sex + texp + extrav + extrav:texp + (1+extrav|class),
summary(cross_level)

Gegenüber dem vorherigen Modell hat sich nur die Spezifikation der Fixed Effects geändert:

1 + sex + texp + extrav + extrav:texp

Wir sehen, dass ganz am Ende noch ein Interaktionsterm, extrav:texp, hinzu gekommen ist.

Hier ist das Ergebnis der Schätzung:

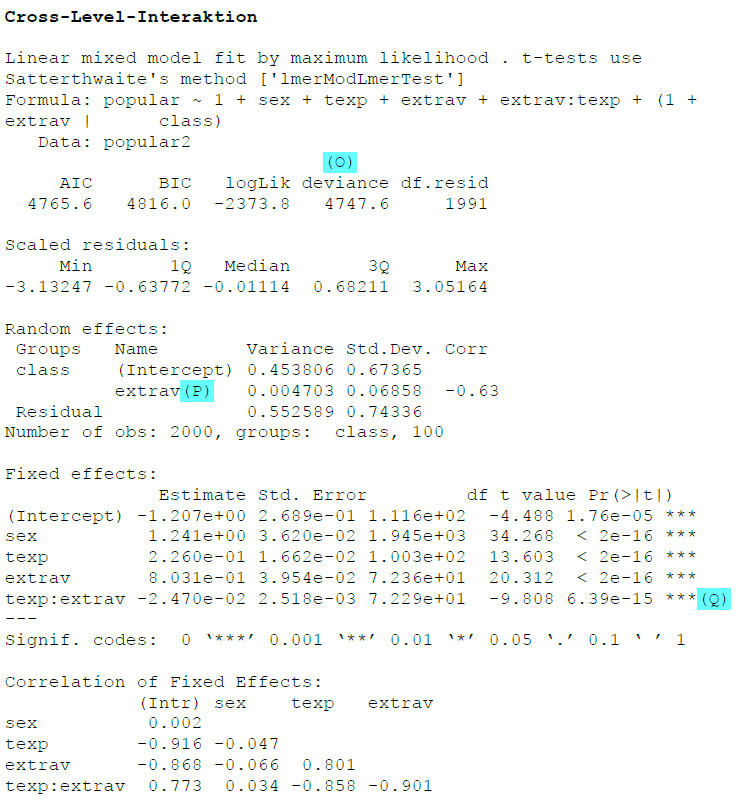
(O): Die Deviance hat sich weiter verringert, von 4812.8 im vorherigen Modell auf 4747.6 im Modell mit Cross Level Interaction.

(P): Die Varianz des Effekts von Extraversion ist deutlich zurückgegangen, von 0.034 im vorherigen Modell auf 0.005 in diesem Modell. Ein Großteil der Schwankung zwischen den Klassen im Extraversionseffekt konnte also durch die Berufserfahrung der Lehrkraft erklärt werden.

(Q): Die Interaktion zwischen Extraversion der Schülerinnen und Schüler und der Berufserfahrung der Lehrkraft ist signifikant negativ. Das bedeutet, dass in Schulklassen mit erfahreneren Lehrkräften der Effekt der Extraversion auf die Popularität der Schülerinnen und Schüler geringer ausfällt als in Schulklassen mit unerfahreneren Lehrkräften.

Wenn Sie für eine Interaktion noch Simple-Slopes auswerten möchten, können Sie das mit dem Package reghelper tun.

Zum einen können Sie die Simple Slopes (Effekte für bestimmte Ausprägungen des Moderators) rechnerisch bestimmen lassen und auf Signifikanz testen:

simple_slopes(cross_level)

Dabei sind die ersten Simple Slopes (1.-3.) die Effekte der Extraversion bei verschiedenen Ausprägungen der Berufserfahrung, während bei den weiteren Simple Slopes (4.-6.) die Betrachtung genau umgekehrt ist. Dort sind die Effekte der Berufserfahrung bei verschiedenen Ausprägungen der Extraversion angegeben. Für unsere Fragestellung sind m.E. die ersten drei Simple Slopes aussagefähiger.

Zum anderen können Sie eine Grafik der Simple Slopes (für +/- 1 SD des Moderators) ausdrucken:

graph_model(cross_level, y = popular, x = extrav, lines = texp)

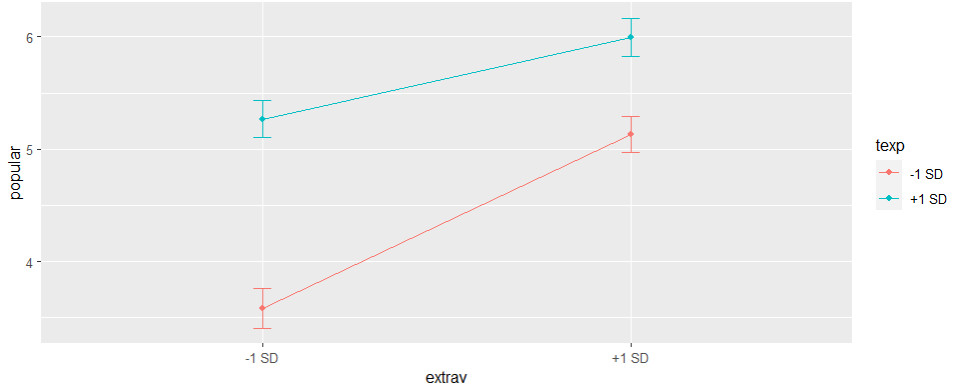
Damit haben wir die Analyse der Daten abgeschlossen. Informationen darüber, wie Sie die Ergebnisse eines HLM-Modells berichten können, finden Sie u.a. im Tutorial Mehrebenenanalyse Ergebnisse berichten sowie bei Dedrick et al. (2009).

5. Vollständiger R-Code

Hier noch einmal im Zusammenhang der gesamte R-Code für dieses Tutorial:

library(lme4)
library(lmerTest)
library(performance)

head(popular2, 5)

# 1. Nullmodell

nullmodell <- lmer(popular ~ 1 + (1|class), data=popular2, REML=F)
summary(nullmodell)
icc(nullmodell)

# 2. Fixed Slopes (Random intercept)

fixed_slopes <- lmer(popular ~ 1 + sex + extrav + texp + (1|class), data=popular2, REML=F)
summary(fixed_slopes)

# 3.a Random Slopes

random_slopes <- lmer(popular ~ 1 + sex + extrav + texp + (1+sex+extrav|class),
data=popular2, REML=F)
summary(random_slopes)

# 3.b Random Slopes nur Extraversion

random_slopes2 <- lmer(popular ~ 1 + sex + extrav + texp + (1+extrav|class),
data=popular2, REML=F)
summary(random_slopes2)

# 4. Cross-Level-Interaktion Extraversion und Teacher Experience

cross_level <- lmer(popular ~ 1 + sex + texp + extrav + extrav:texp +
(1+extrav|class),data=popular2, REML=F)
summary(cross_level)

simple_slopes(cross_level)
graph_model(cross_level, y = popular, x = extrav, lines = texp)

6. Ausblick

Mit diesem Tutorial haben Sie einen ersten Überblick darüber, wie Sie mit R und dem lme4 Modul eine Mehrebenenanalyse durchführen können. Um jedoch so ein Modell z.B. für Ihre Abschlussarbeit zu schätzen, benötigen Sie noch eine Reihe weiterer Kompetenzen. für die es mehrere Folgetutorials gibt:

• Mehrebenenanalyse (mit R) 2: Voraussetzungen prüfen
• Mehrebenenanalyse (mit R) 3: Zentrierung
• Mehrebenenanalyse (mit R) 4: p-Values Random Effects ermitteln
• Mehrebenenanalyse (mit R) 5: Ergebnisse berichten
• Mehrebenenanalyse (mit R) 6: Robuste Schätzung
• Mehrebenenanalyse (mit R) 7: Grundlagen mit nlme
• Formeln Mehrebenenanalyse verstehen: Videotutorial mit graphischer Erklärung der Formeln einer Mehrebenenanalyse (nicht R-spezifisch)

7. Literatur

Dedrick, R. F., Ferron, J. M., Hess, M. R., Hogarty, K. Y., Kromrey, J. D., Lang, T. R., Niles, J. D., & Lee, R. S. (2009). Multilevel modeling: A review of methodological issues and applications. Review of Educational Research, 79(1), 69-102. https://doi.org/10.3102/0034654308325581

Enders, C. K., & Tofighi, D. (2007). Centering predictor variables in cross-sectional multilevel models: a new look at an old issue. Psychological Methods, 12(2), 121-138. https://doi.org/10.1037/1082-989X.12.2.121

Hox, J. J., Moerbeek, M., & Van de Schoot, R. (2017). Multilevel analysis: Techniques and applications (3rd edition). Routledge.