SPSS: Double Mean Centering for a Moderated SEM Model in AMOS

Arndt Regorz, M.Sc. Psychology, 04/24/2023

Are you interested in performing moderation analysis using a full structural equation model (SEM) with latent variables? If so, you're in the right place. Modeling a latent interaction variable is not easy in SEM, but it's a necessary step to conduct moderation analysis.

Here we will dive into the nuances of incorporating latent interaction variables in SEM and describe a procedure from the literature that can be used to model these interactions effectively, i.e. double mean centering. You will get the necessary SPSS-code for double mean centering the indicator variables for a latent interaction so that you can use them in your AMOS model.

Moderation in SEM with Double Mean Centering (latent interactions) - Basics.

Performing a moderation analysis with a full structural equation model (SEM) with latent variables can be challenging, especially the modeling of a latent interaction variable which is necessary to do so. In the context of moderated regression, it is well known that moderation can be tested by including the independent variable (IV), the moderator, and the interaction between IV and moderator in the multiple regression.

This procedure can in principle also be used in SEM, but indicator variables for the latent interaction must be calculated. Various procedures for modeling latent interactions are discussed in the literature.

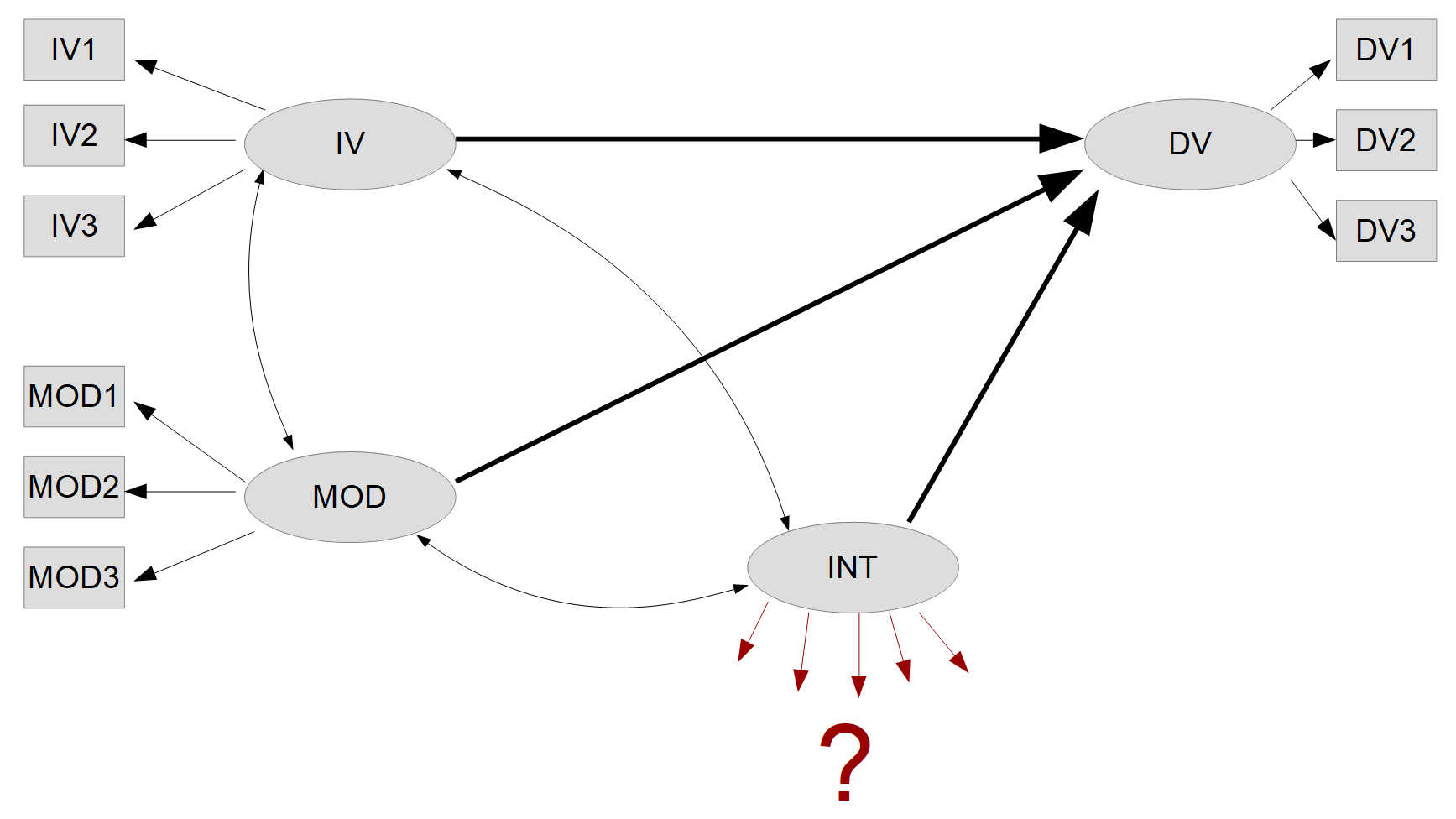
A common method for modeling interaction effects in an SEM is the double mean centering method. Here are the steps required to apply the double mean centering method for a moderator analysis:

Step 1: Centering the indicator variables
To use the double mean centering method, the indicator variables that will be included in the SEM model are first centered. Centering means that the average of the variables is set to zero by subtracting from each data point the average of the respective variable over all observations.

Step 2: Formation of the interaction terms
Once the indicator variables have been centered, the interaction terms can be created. This is done by multiplying the centered values of the moderator's indicators by the centered values of the independent variable's indicators.

Step 3: Centering the interaction terms
After the interaction terms are created, they are also centered again (hence double mean centering).

Step 4: Fitting the interaction terms into the SEM model
After the interaction terms have been centered, they can be used in the SEM model as indicators for the latent interaction variable.

Step 5: Consideration of error covariances
When estimating such a model, it is important to note that several of the (double-centered) interaction indicators have commonalities with each other. For example, in a model with three indicators each for IV and moderator, the interaction variable IV1-MOD1 shares a component with the interactions IV1-MOD2, IV1-MOD3, IV2-MOD1, and IV3-MOD1. Therefore, one must expect that the error terms of these variables also covary with each other. If this is not taken into account, the model fit may deteriorate accordingly.

A relevant paper about the double mean centering method for modeling latent interactions can be found here:

Lin, G. C., Wen, Z., Marsh, H. W., & Lin, H. S. (2010). Structural equation models of latent interactions: Clarification of orthogonalizing and double-mean-centering strategies. Structural Equation Modeling, 17(3), 374-391. https://doi.org/10.1080/10705511.2010.488999

SPSS Code for Double Mean Centering

Here is the annotated SPSS code for double mean centering. The code example is based on having an IV with three indicator variables (IV1, IV2, IV3) and a moderator with three indicator variables (MOD1, MOD2, MOD3). If you have different measurement models for IV or for moderator, then you will have to adjust the code accordingly.

*1. Mean centering of the indicators for IV and MOD.

* Means of the indicator variables.
AGGREGATE
/OUTFILE=* MODE=ADDVARIABLES OVERWRITE = YES
/BREAK=
/IV1_mean=MEAN(IV1)
/IV2_mean=MEAN(IV2)
/IV3_mean=MEAN(IV3)
/MOD1_mean=MEAN(MOD1)
/MOD2_mean=MEAN(MOD2)
/MOD3_mean=MEAN(MOD3).

*Mean centering.
COMPUTE IV1_mc=IV1 - IV1_mean.
COMPUTE IV2_mc=IV2 - IV2_mean.
COMPUTE IV3_mc=IV3 - IV3_mean.
COMPUTE MOD1_mc=MOD1 - MOD1_mean.
COMPUTE MOD2_mc=MOD2 - MOD2_mean.
COMPUTE MOD3_mc=MOD3 - MOD3_mean.
EXECUTE.

*2. Calculating interaction terms.

COMPUTE Int_IV1_MOD1=IV1_mc * MOD1_mc.
COMPUTE Int_IV1_MOD2=IV1_mc * MOD2_mc.
COMPUTE Int_IV1_MOD3=IV1_mc * MOD3_mc.
COMPUTE Int_IV2_MOD1=IV2_mc * MOD1_mc.
COMPUTE Int_IV2_MOD2=IV2_mc * MOD2_mc.
COMPUTE Int_IV2_MOD3=IV2_mc * MOD3_mc.
COMPUTE Int_IV3_MOD1=IV3_mc * MOD1_mc.
COMPUTE Int_IV3_MOD2=IV3_mc * MOD2_mc.
COMPUTE Int_IV3_MOD3=IV3_mc * MOD3_mc.
EXECUTE.

*3. Mean centering of the interaction terms.

* Means for the interaction
AGGREGATE
/OUTFILE=* MODE=ADDVARIABLES OVERWRITE = YES
/BREAK=
/Int_IV1_MOD1_mean=MEAN(Int_IV1_MOD1)
/Int_IV1_MOD2_mean=MEAN(Int_IV1_MOD2)
/Int_IV1_MOD3_mean=MEAN(Int_IV1_MOD3)
/Int_IV2_MOD1_mean=MEAN(Int_IV2_MOD1)
/Int_IV2_MOD2_mean=MEAN(Int_IV2_MOD2)
/Int_IV2_MOD3_mean=MEAN(Int_IV2_MOD3)
/Int_IV3_MOD1_mean=MEAN(Int_IV3_MOD1)
/Int_IV3_MOD2_mean=MEAN(Int_IV3_MOD2)
/Int_IV3_MOD3_mean=MEAN(Int_IV3_MOD3).

*Mean centering.
COMPUTE Int_IV1_MOD1_mc=Int_IV1_MOD1 - Int_IV1_MOD1_mean.
COMPUTE Int_IV1_MOD2_mc=Int_IV1_MOD2 - Int_IV1_MOD2_mean.
COMPUTE Int_IV1_MOD3_mc=Int_IV1_MOD3 - Int_IV1_MOD3_mean.
COMPUTE Int_IV2_MOD1_mc=Int_IV2_MOD1 - Int_IV2_MOD1_mean.
COMPUTE Int_IV2_MOD2_mc=Int_IV2_MOD2 - Int_IV2_MOD2_mean.
COMPUTE Int_IV2_MOD3_mc=Int_IV2_MOD3 - Int_IV2_MOD3_mean.
COMPUTE Int_IV3_MOD1_mc=Int_IV3_MOD1 - Int_IV3_MOD1_mean.
COMPUTE Int_IV3_MOD2_mc=Int_IV3_MOD2 - Int_IV3_MOD2_mean.
COMPUTE Int_IV3_MOD3_mc=Int_IV3_MOD3 - Int_IV3_MOD3_mean.
EXECUTE.

As a result, we now have nine double-centered indicator variables for the latent interaction between latent variables IV and MOD. We can use these in AMOS for the measurement model of the latent interaction. Thus, in AMOS:

IV is measured by: IV1, IV2, IV3

The moderator is measured by: MOD1, MOD2, MOD3

The interaction is measured by: Int_IV1_MOD1_mc, Int_IV1_MOD2_mc, Int_IV1_MOD3_mc, Int_IV2_MOD1_mc, Int_IV2_MOD2_mc, Int_IV2_MOD3_mc, Int_IV3_MOD1_mc, Int_IV3_MOD2_mc, Int_IV3_MOD3_mc.

In addition, as explained above in step 5, you still need to include error covariances between those interaction variables that share a common element. To do this, simply draw corresponding correlation arrows (double-headed arrows) in AMOS between the indicator variables of the relevant interactions.

In the example here with three indicators each for the independent variable and the moderator, each interaction indicator must have correlation arrows to four other interaction indicators. Using the example of interaction IV2MOD3:
Arrows to IV2MOD1 and IV2MOD2, because the element IV2 is common.
Arrows to IV1MOD3 and IV3MOD3, because the element MOD3 is common.