Wie interpretiert man die Tabelle "Kollinearitätsdiagnose" in SPSS?

Arndt Regorz, Dipl. Kfm. & M.Sc. Psychologie, 19.11.2019


Wenn im Rahmen der multiplen Regression die Option "Kollinearitätsdiagnose" gewählt wird, werden zwei zusätzliche Informationen in der SPSS-Ausgabe aufgeführt.

Zunächst erscheinen in der Tabelle "Koeffizienten" ganz rechts zwei zusätzliche Spalten unter der Überschrift "Kollinearitätsstatistik": "Toleranz" und "VIF".

Außerdem, und das ist unser Thema hier, erscheint unter der Koeffizienten-Tabelle eine neue Tabelle: "Kollineariätsdiagnose":

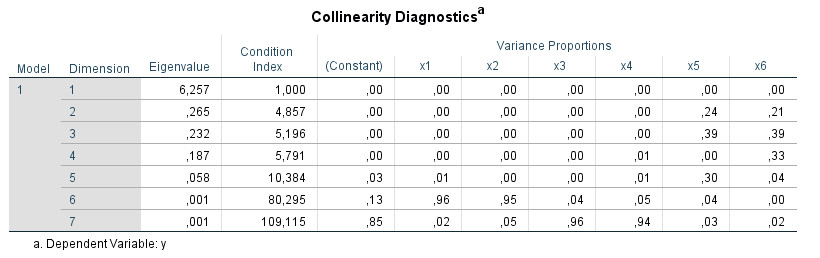
Collinearity diagnostics table SPSS


(Alle Bilder in diesem Tutorial sind aus technischen Gründen mit englischsprachigen Tabellenbeschriftungen versehen.)

Die Interpretation dieser SPSS-Tabelle ist oft unbekannt und es ist relativ schwierig, klare Informationen darüber zu finden. Das folgende Tutorial zeigt Ihnen, wie Sie für die Kollinearitätsdiagnose den SPSS Output verwenden können, um Multikollinearität in Ihren multiplen Regressionen weiter zu analysieren. Das Tutorial basiert auf SPSS Version 25.

Inhalt

  1. YouTube Video-Tutorial"
  2. Spalte "Dimension"
  3. Spalte "Eigenwert"
  4. Spalte "Konditionsindex"
  5. Bereich "Varianzanteile"
  6. Hierarchische Regression
  7. Wie man die Information nutzt
  8. Beispiel
  9. Quellen

1. YouTube Video-Tutorial

Das folgende Video erklärt (auf Englisch), wie man die Tabelle "Kollinearitätsdiagnose" interpretiert.

(Hinweis: Mit Anklicken des Videos wird ein Angebot des Anbieters YouTube genutzt.)

2. Spalte "Dimension"

Ähnlich (aber nicht identisch) wie bei einer Faktoranalyse oder PCA (Hauptkomponentenanalyse) wird versucht, aus den Prädiktoren Dimensionen mit unabhängigen Informationen zu bestimmen. Genauer gesagt, wird eine singular value decomposition (Wikipedia, n.d.) der X-Matrix ohne ihre vorherige Zentrierung durchgeführt (Snee, 1983).

3. Spalte "Eigenwert"

Mehrere Eigenwerte nahe bei Null sind ein Hinweis auf Multikollinearität (IBM, n.d.). ("Eigenwert" ist ein Begriff aus der Matrixalgebra, den zu erklären den Rahmen dieses Tutorials sprengen würde. Aber man muss den Begriff auch nicht mathematisch verstehen, um die Informationen der Kollinearitätsdiagnose sinnvoll nutzen zu können.) Da "nahe bei" etwas ungenau ist, ist es besser, die nächste Spalte mit dem Condition Index für die Diagnose zu verwenden - dort gibt es nämlich konkrete Cut-off-Werte.

4. Spalte "Konditionsindex"

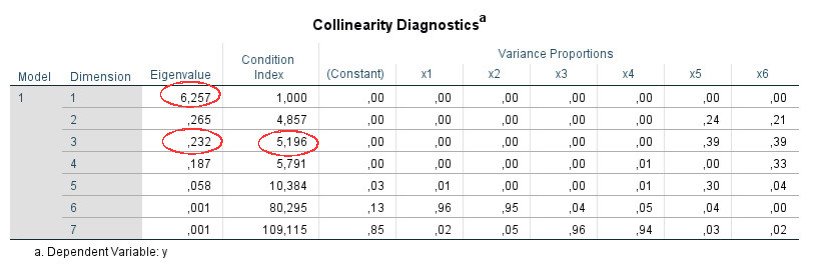
Der Konditionsindex wird je Dimension aus den Eigenwerten berechnet. Der Konditionsindex für eine Dimension ergibt sich dabei aus der Quadratwurzel des Verhältnisses des größten Eigenwertes (Dimension 1) zum Eigenwert der Dimension. image Condition index collinearity diagnostics SPSS


In der obigen Tabelle z.B. für Dimension 3:
Eigenwert Dimension 1: 6.257
Eigenwert Dimension 3: 0.232
Eigenwert Dimension 1 / Eigenwert Dimension 3: 26.970
Quadratwurzel darauf (=Konditionsindex): 5.193
(der Unterschied zum Output von 5.196 ist vermutlich ein Rundungsfehler)

Wichtiger als die Berechnung ist die Interpretation des Konditionsindex. Werte über 15 können auf Multikollinearitätsprobleme hinweisen, Werte über 30 sind ein sehr starkes Zeichen für Probleme mit Multikollinearität (IBM, n.d.). Für alle Zeilen, in denen entsprechend hohe Werte für den Konditionsindex auftreten, sollte man dann den nächsten Abschnitt mit den "Varianzanteilen" betrachten.

5. Bereich "Varianzanteile"

Als nächstes betrachten Sie die Varianzanteilsmatrix des Regressionskoeffizienten. Hier wird für jeden Regressionskoeffizienten seine Varianz auf die verschiedenen Eigenwerte verteilt (Hair, Black, Babin, & Anderson, 2013). Wenn Sie sich die Zahlen in der Tabelle ansehen, sehen Sie, dass sich die Varianzanteile spaltenweise zu Eins summieren.

Gemäß Hair et al. (2013) suchen Sie für jede Zeile mit einem hohen Konditionsindex nach Werten über .90 in den Varianzanteilen. Wenn Sie zwei oder mehr Werte über .90 in einer Zeile finden, können Sie davon ausgehen, dass es ein Kollinearitätsproblem zwischen diesen Prädiktoren gibt. Wenn nur ein Prädiktor in einer Zeile einen Wert über .90 hat, ist dies kein Zeichen für Multikollinearität.

Nach meiner Erfahrung führt diese Regel jedoch nicht immer zur Identifizierung der Prädiktoren mit Kollinearität. Es ist durchaus möglich, mehrere Variablen mit hohen VIF-Werten zu finden, ohne Zeilen mit Paaren (oder größeren Gruppen) von Prädiktoren mit Werten über .90 zu finden. In diesem Fall würde ich auch nach Paaren in einer Zeile mit Varianzanteilen über z.B. .80 oder .70 suchen.

6. Hierarchische Regression

Wenn Sie eine hierarchische Regression durchführen, erscheinen die entsprechenden Werte der Tabelle "Kollinearitätsdiagnose" für jeden Regressionsschritt separat ("Modell 1", "Modell 2"):

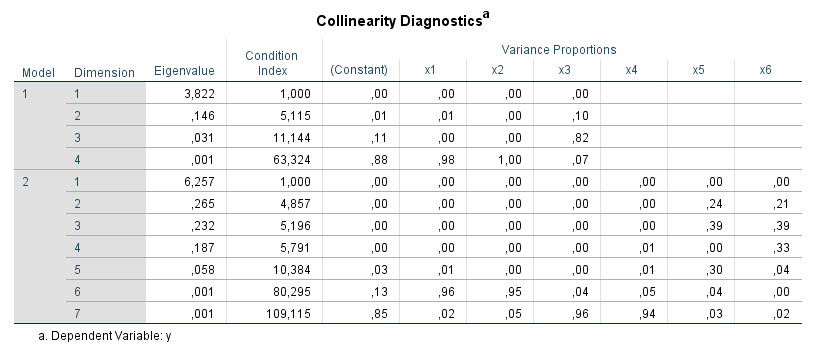
Table Collinearity diagnostics hierarchical regression


Ich würde in erster Linie die Daten für den letzten Schritt betrachten oder im Allgemeinen die Daten für die Schritte, die Sie berichten und für Ihre Hypothesentests interpretieren.

7. Wie man die Information nutzt

Wenn ich eine multiple Regressionsausgabe auf Multikollinearität analysieren möchte, gehe ich so vor:

  1. Ich betrachte den Wert "VIF" in der Tabelle "Koeffizienten". Wenn dieser Wert für alle Prädiktoren kleiner als 10 ist, ist das Thema für mich geschlossen.
  2. Wenn es nur maximal zwei Werte des VIF über 10 gibt, gehe ich davon aus, dass das Kollinearitätsproblem zwischen diesen beiden Werten besteht und interpretiere nicht die Tabelle "Kollinearitätsdiagnose". Wenn es jedoch mehr als zwei Prädiktoren mit einem VIF über 10 gibt, dann werde ich mir die Kollinearitätsdiagnostik näher ansehen.
  3. Ich identifiziere die Zeilen mit einem Konditionsindex über 15.
  4. In diesen Zeilen prüfe ich, ob es mehr als eine Spalte (mehr als einen Prädiktor) mit Werten über .90 in den Varianzanteilen gibt. In diesem Fall gehe ich von einem Kollinearitätsproblem zwischen den Prädiktoren aus, die diese hohen Werte haben.
  5. Wenn nur ein Prädiktor in einer Zeile einen hohen Wert hat (über .90), ist dies für mich nicht relevant.
  6. Wenn ich die Quelle der Multikollinearität noch nicht identifizieren konnte, weil es keine Zeile mit mehreren Varianzanteilen über .90 gibt, reduziere ich dieses Kriterium und betrachte beispielsweise auch Prädiktorenpaare (oder Gruppen von Prädiktoren) mit Werten über .80 oder .70.

8. Beispiel

Schritt 1: Es gibt Prädiktoren mit einem VIF über 10 (x1, x2, x3, x4).

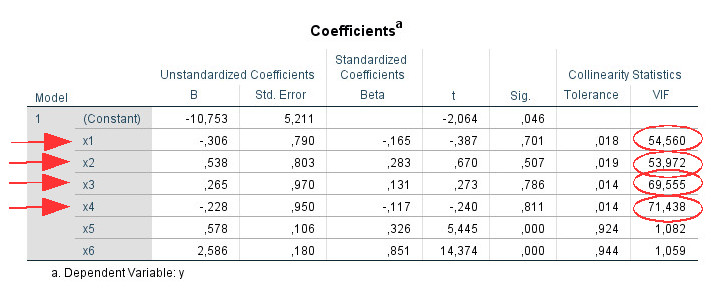
SPSS Collinearity statistics example VIF


Schritt 2: Es gibt mehr als zwei Prädiktoren (hier: vier), auf die das zutrifft. Daher betrachte ich die Tabelle zur Kollinearitätsdiagnose.

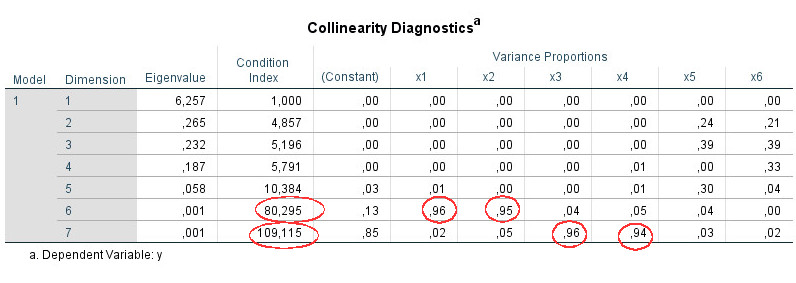
SPSS Collinearity diagnostics table example


Schritt 3: Dimensionen 6 und 7 zeigen einen Konditionsindex über 15.

Schritt 4:Für jede dieser zwei Dimensionen suche ich nach Werten über .90. Für Dimension 6 finden sich diese für die Prädiktoren x1 and x2, für Dimension 7 für die Prädiktoren x3 and x4. Auf dieser Basis nehme ich an, dass es hier zwei verschiedene Kollinearitätsprobleme gibt: zwischen x1 und x2 und zwischen x3 and x4. (Wenn hingegen die Werte über .90 für diese vier Prädiktoren alle in einer Zeile gewesen wären, hätte das auf ein einziges Multikollinearitätsproblem mit allen vier Variablen zusammen hingedeutet.)

Schritte 5 and 6 sind in diesem Beispiel nicht relevant.

9. Quellen

Hair, J. F., Black, W. C., Babin, B. J., & Anderson, R. E. (2013). Multivariate data analysis: Advanced diagnostics for multiple regression [Online supplement]. Retrieved from http://www.mvstats.com/Downloads/Supplements/Advanced_Regression_Diagnostics.pdf

IBM (n.d.). Collinearity diagnostics. Retrieved August 19, 2019, from https://www.ibm.com/support/knowledgecenter/en/SSLVMB_23.0.0/spss/tutorials/reg_cars_collin_01.html

Snee, R. D. (1983). Regression Diagnostics: Identifying Influential Data and Sources of Collinearity. Journal of Quality Technology, 15, 149-153. doi:10.1080/00224065.1983.11978865

Wikipedia (n.d.). Singular value decomposition. Retrieved August 19, 2019, from https://en.wikipedia.org/wiki/Singular_value_decomposition