Ausreißer und Ausreißerdiagnostik bei der Regression

Arndt Regorz, Dipl. Kfm. & MSc. Psychologie, Stand: 20.08.2021

Eine Voraussetzung für die lineare Regression ist, dass es keine zu starken Ausreißer in den Daten gibt. Dieses Tutorial erklärt, warum Ausreißer ein Problem sein können für Ihre Regression, wie Sie Ausreißer diagnostizieren und wie Sie damit umgehen können, wenn Sie Ausreißer in Ihren Daten haben.

1. Warum sind Ausreißer ein Problem?

Extreme Ausreißer können aus zwei Gründen ein Problem sein:

Sie können die Lage der Regressionsgeraden und damit die Regressionsgewichte stark beeinflussen.
Sie deuten häufig auf eine Verletzung der Normalverteilungsannahme

Das Problem der Normalverteilung habe ich in einem anderen Tutorial erklärt, hier wollen wir uns vor allem mit dem überproportionalen Einfluss von Ausreißern beschäftigen und warum das ein Problem ist.

Die lineare Regression wird mit der Kleinst-Quadrate-Methode (least squares) geschätzt. Dabei versucht der Lösungsalgorithmus, die quadratischen Residuen zu minimieren, also die quadrierten Differenzen zwischen tatsächlichen Werten und geschätzten Werten auf der Kriteriumsvariable. Und diese Optimierung anhand der quadrierten Abweichungen führt dazu, dass starke Abweichungen einen überproportionalen Einfluss haben, denn z.B. ein doppelt so großes Residuum hat durch die Quadrierung einen viermal so großen Einfluss.

Insbesondere bei kleinen Stichproben kann sogar ein einziger extremer Ausreißer zu völlig anderen Ergebnissen führen. Hier ein (Extrem-)Beispiel mit N = 20, einem Ausreißer und der resultierenden Regressionsgerade. Als Ergebnis resultiert ein beta = .686 mit p = .001.

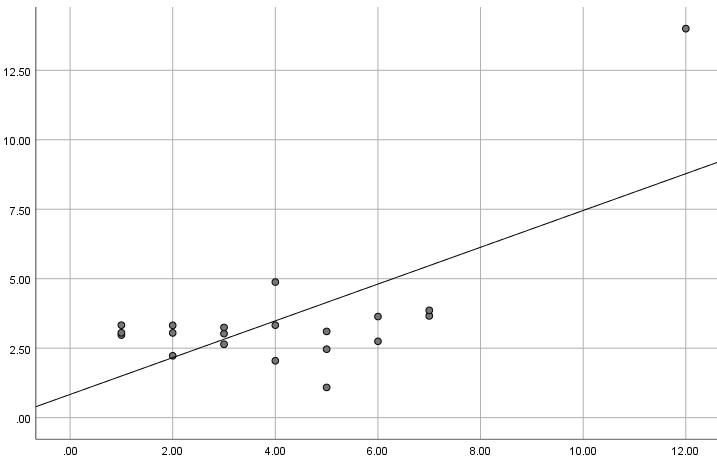
Und hier das gleiche Modell ohne diesen Ausreißer. Jetzt erhält man ein nicht signifikantes beta = .108 mit p = .661.

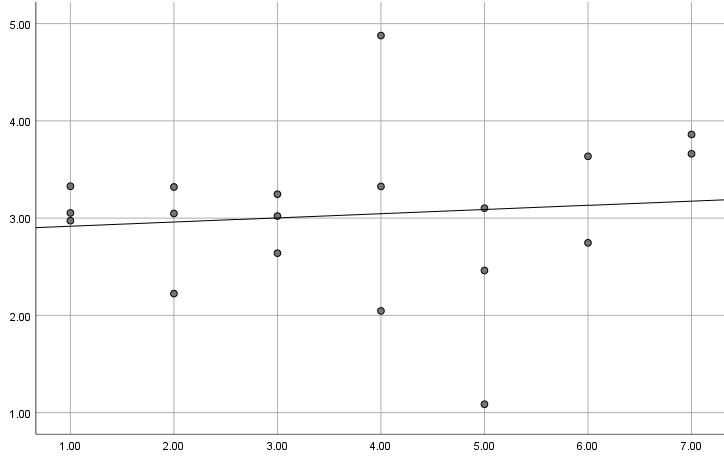
Wenn man dieses Problem ignoriert, kann man also zu völlig falschen Schlussfolgerungen über die in der Regression untersuchten Zusammenhänge kommen. Dafür reicht im schlimmsten Fall schon ein einziger Ausreißer.

2. Ausreißerdiagnostik

Zur Ausreißerdiagnostik sind in der Literatur zahlreiche Kennzahlen entwickelt worden, mit denen man prüfen kann, ob eine Beobachtung ein möglicherweise problematischer Ausreißer ist. Nachfolgend werden davon vier vorgestellt, die ich aus verschiedenen Gründen gerne nutze. Für die Cut-off-Werte, ab denen man von einem problematischen Ausreißer ausgeht, gibt es in der Literatur verschiedene Werte.

Standardisierte Residuen

Die einfachste Möglichkeit ist die Betrachtung der standardisierten Residuen, zumindest wenn man mit SPSS arbeitet. Denn diese Analyse ist in den Regressionsdialog integriert und man bekommt am Ende sogar eine Liste mit den Fällen, die auf Basis der standardisierten Residuen als Ausreißer einzuschätzen sind. Dabei kann man einstellen, ab welchem Wert der standardisierten Residuen ein Fall ein Ausreißer sein soll.

Häufig sieht man die Praxis, dass Fälle mit standardisierten Residuen von absolut größer als 3.0 als Ausreißer angesehen werden – auch deshalb, weil das die Standardeinstellung bei SPSS ist. Das ist aber nicht völlig unproblematisch: Es hängt eigentlich auch von der Stichprobengröße ab. In einer kleinen Stichprobe, wie z.B. oben mit N = 20 wäre ein standardisiertes Residuum von größer als 3.0 ganz deutlich ein extremer Ausreißer. Bei einer Stichprobe von z.B. N = 800 hingegen wären zwei oder drei solche Werte auch bei Geltung der Normalverteilungsannahme zu erwarten.

Aus diesem Grund sind die drei nachfolgend dargestellten diagnostischen Werte aus meiner Sicht vorzuziehen.

In unserem o.g. Beispielfall hätte der im Streudiagramm sichtbare extreme Ausreißer ein standardisiertes Residuum von 2.72, würde bei Verwendung der Grenze von +/- 3 also noch nicht einmal als Ausreißer auffallen (was mich überrascht hat)!

Hebelwerte (leverage)

Ausreißer können auf Seiten der Prädiktoren (UV) und auf Seiten des Kriteriums (AV) auftreten. Die Hebelwerte betrachten die Seite der Prädiktoren und sollen Fälle identifizieren, die eine sehr starke Wirkung (Hebel) auf die Regressionsgerade haben, weil sie hinsichtlich des Prädiktors stark vom Mittelwert abweichen.

Für diesen Kennwert sind bei kleinen Stichproben Werte größer als 3k/n als Problem anzusehen (bei großen Stichproben Werte oberhalb von 2k/n), mit k = Anzahl der Prädiktoren im Modell und n = Stichprobenumfang (Urban & Mayerl, 2018). In unserem Beispiel oben wäre als einfache Regression k = 1 und der Stichprobenumfang n = 20, so dass in diesem Fall Werte größer 3 * 1 / 20 = 0.15 ein Indiz für einen Ausreißer wären.

In unserem o.g. Beispielfall hätte der im Streudiagramm sichtbare Ausreißer einen Hebelwert von 0.46, würde also deutlich als Ausreißer identifiziert. (Die anderen Fälle haben alle Hebelwerte unter 0.08, sind also unproblematisch).

Standardisiertes DifBeta

Das standardisierte DifBeta prüft direkt, ob ein Fall einen überproportionalen Einfluss auf die Lage der Regressionsgerade hat.

Für diesen Kennwert sind Grenzwerte für problematische Fälle +/-1 bei kleinen Stichproben, bei großen Stichproben Werte +/-2 / sqrt(N) (Urban & Mayerl, 2018).

In unserem o.g. Beispielfall hätte der im Streudiagramm sichtbare Ausreißer ein standardisiertes DifBeta von 8.92, würde also sehr deutlich als Ausreißer identifiziert. (Die anderen Fälle hier liegen vom Absolutbetrag alle unter 0.30, sind also völlig unproblematisch.)

Bei SPSS muss man berücksichtigen, dass beim Aufruf des standardisierten DifBeta zwei Werte angegeben werden – ein Wert für das Intercept und ein Wert für die Steigung der Regressionsgerade, und dieser zweite Wert für die Steigung ist der interessante.

Cook's Distanz

Die Cook's Distanz prüft gleichzeitig, ob ein Fall ein Ausreißer bezüglich der Prädiktoren und bezüglich des Kriteriums (bzw. des Residuums) ist und wäre insofern meine Wahl, falls ich nur einen einzigen Kennwert beurteilen möchte.

Cook's Distanz ist näherungsweise F-verteilt. Die kritische Schwelle sind Werte über dem 0.50 Quantil einer F-Verteilung mit df1 = k +1 und df2 = n – k – 1 (k = Anzahl der Prädiktoren, n = Stichprobengröße).

Das sieht jetzt viel komplizierter aus, als es ist. In unserem Beispiel oben wäre k = 1 (ein Prädiktor) und n = 20. Damit ergeben sich für die Freiheitsgrade:
df1 = 1 + 1 = 2
df2 = 20 – 1 – 1 = 18

Wir müssen also nur noch den F-Wert für eine Wahrscheinlichkeit von 0.50 und df1= 2 und df2 = 18 bestimmen. Dafür gibt es F-Wert-Rechner im Internet, z.B. https://stattrek.com/online-calculator/f-distribution.aspx

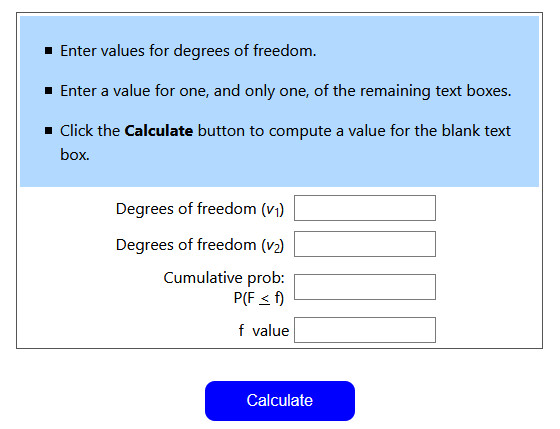
Wenn man dort die drei o.g. Werte eingibt (v1, v2, Cumulative prob.) und auf „Calculate“ klickt, erhält man einen für unsere Beispieldaten kritischen F-Wert von 0.72. Fälle mit einer Cook's Distanz über diesem Wert sind für unser Beispiel problematisch. (Hinweis: Bitte denken Sie daran, auf dieser englischsprachigen Internetseite die Wahrscheinlichkeit mit einem Punkt anzugeben, also 0.50 statt 0,50 – sonst funktioniert der Rechner nicht.)

Wenn man mit SPSS arbeitet, könnte man diesen F-Wert auch über die Syntax anfordern (in der Klammer des Befehls ist zuerst das 0.50 Quantil angegeben und dann die beiden Angaben zu den Freiheitsgraden):

COMPUTE fkrit = idf.f(0.5, 2, 18).
EXECUTE.

Der Wert wird dann als neue Datenspalte in den Datensatz geschrieben.

In unserem o.g. Beispielfall hätte der im Streudiagramm sichtbare Ausreißer eine Cook's Distanz von 7.75, würde also sehr deutlich als Ausreißer identifiziert (für alle anderen Fälle liegt im Beispiel Cook's Distanz bei unter 0.08 und ist insofern dort völlig unproblematisch).

Vorab Boxplots der Variablen?

Mitunter sieht man auch das Vorgehen, dass statt der o.g. Kennwerte einfach bereits vor der Regression Boxplots der verschiedenen Prädiktorvariablen (UV) und der Kriteriumsvariablen (AV) aufgerufen werden, um Ausreißer zu diagnostizieren. Insbesondere bei der Kriteriumsvariable ist davon abzuraten, da hier für die Ausreißerstellung nicht der Wert der Variable sondern das Residuum (Unterschied zwischen Wert und vorhergesagtem Wert) entscheidend ist. Und auch die Boxplots für einzelne Prädiktorvariablen sind aus meiner Sicht deutlich weniger geeignet als der Hebelwert, um extrem vom Mittelwert abweichende Fälle hinsichtlich der Kombination der Prädiktoren zu identifizieren.

3. Aufruf Ausreißerdiagnostik mit SPSS

Die standardisierten Residuen kann man unter "Fallweise Diagnose" aus dem Regressionsdialog aufrufen in der Dialogbox "Statistiken“.

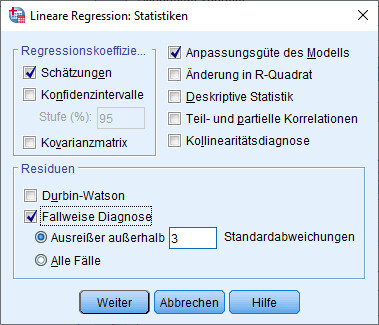
Man erhält dann auf jeden Fall folgende Tabelle (wobei die Anzahl der Zeilen sich je nach Aufruf unterscheiden kann).

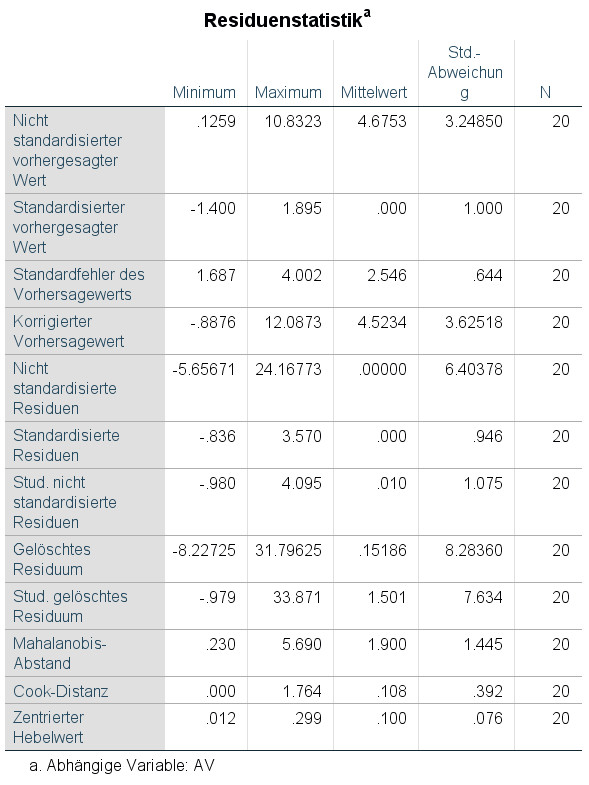
Interessanter jedoch ist: Wenn ein oder mehrere Residuen absolut größer als der eingestellte Grenzwert (Voreinstellung in SPSS: 3) sind, dann erhält man noch eine Liste der betroffenen Fälle:

Die anderen drei diagnostischen Werte (und noch viele mehr) erhält man aus dem Regressionsdialog in der Dialogbox „Speichern“

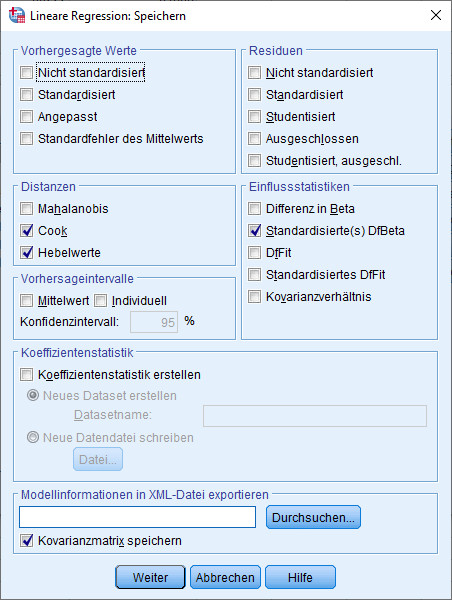
Wenn man die Regression durchgeführt hat, werden die ausgewählten Kennzahlen gespeichert im eigenen Datensatz ganz rechts unter:
COO1: Cook's Distanz
LEV1: Hebelwert (leverage)
SDB1_1: Standardisiertes DifBeta UV

(Die Zahl 1 am Ende der Variablennamen wurde automatisch generiert von SPSS. Wenn man zwei Mal z.B. Cook's Distanz speichern lässt, wird die zweite als COO2 gespeichert, usw.)

4. Aufruf Ausreißerdiagnostik mit R

Die Basis für die folgende Ausreißerdiagnostik ist jeweils ein geschätztes Regressionsmodell, also z.B. als Ergebnis so eines Aufrufs:
reg.fit <- lm(AV ~ UV1 + UV2 + UV3, data=mein.datensatz)

Für die Diagnose wird jeweils das R-Package olsrr verwendet. Dieses muss wie jedes Package einmalig installiert werden (install.packages) und dann jeweils mit library geladen werden.

Studentisierte Residuen

library(olsrr)
ols_plot_resid_stud(reg.fit)

Cook's Distanz

library(olsrr)
ols_plot_cooksd_chart(reg.fit)

Outlier & Leverage

library(olsrr)
ols_plot_resid_lev(reg.fit)

DiffBETAS

library(olsrr)
ols_plot_dfbetas(reg.fit)

5. Umgang mit Ausreißern

Für den Umgang mit Ausreißern gibt es viele verschiedene mögliche Vorgehensweisen, über die es in der Literatur auch keinen Konsens gibt.

Einen Überblick über Ihre möglichen Handlungsoptionen finden Sie in meinem Tutorial Umgang mit Ausreißern bei der Regressionsanalyse.

6. Quellen

Baltes-Götz, B. (2019). Lineare Regressionsanalyse mit SPSS (Rev. 190522). Universität Trier. https://www.uni-trier.de/fileadmin/urt/doku/linreg/linreg.pdf

Glen, S. (n.d). What is Cook’s Distance? https://www.statisticshowto.com/cooks-distance/

Hebbali, A. (2020). Package 'olsrr'. CRAN. https://cran.r-project.org/web/packages/olsrr/olsrr.pdf

McDonald, B. (2002). A teaching note on Cook's distance - a guideline. Research Letters in the Information and Mathematical Sciences, 3, 122-128. https://mro.massey.ac.nz/handle/10179/4352

Urban, D., & Mayerl, J. (2018). Angewandte Regressionsanalyse: Theorie, Technik und Praxis. Springer VS.